Unraveling the Connection Between 1/89 and the Fibonacci Sequence
Written on
Chapter 1: Introduction to the Fibonacci Sequence
This article aims to delve into how the decimal expansion of certain fractions can lead to the Fibonacci sequence. To begin, let's examine the decimal representation of 1/89:
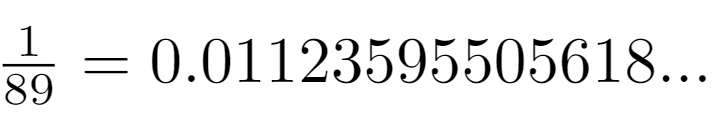
Before we continue, let's briefly review the Fibonacci sequence. It starts with the numbers 0 and 1, and each subsequent number is the sum of the two preceding ones. This results in the sequence: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, and so on.
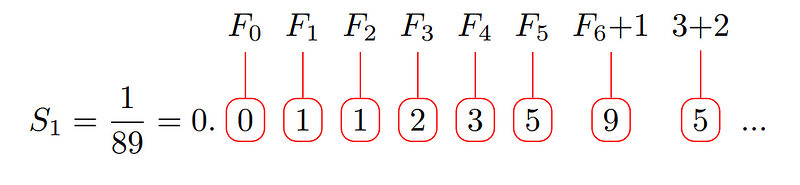
(A quick note on notation: F? = Fib(n) = nth Fibonacci number)
When you compare the Fibonacci sequence with the decimal expansion of 1/89, you might be able to identify some intriguing connections.
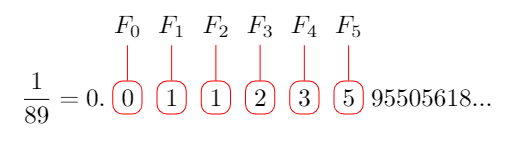
At first glance, the pattern may seem inconsistent. The next digit should be 8, which corresponds to Fib(6). Yet, upon closer inspection, you can see that 9 emerges from 8 and the tens place of 13, representing Fib(7).
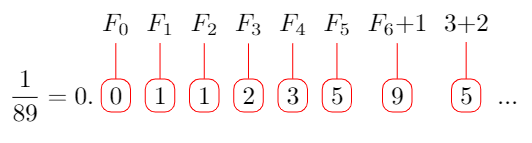
This observation suggests that each Fibonacci number occupies a single digit space. As Fibonacci numbers grow larger than one digit, they begin to overlap with the preceding digit, complicating the tracing of which Fibonacci numbers correspond to specific decimal positions.
(We will address the issue of digit overflow later.)
Working Backwards
While we have identified a pattern, we must verify whether it persists in the infinite expansion of 1/89. To establish this relationship, a complete proof should begin with an infinite summation of Fibonacci numbers divided by increasing powers of 10, demonstrating that this expression equals 1/89. We can start with the following expression:
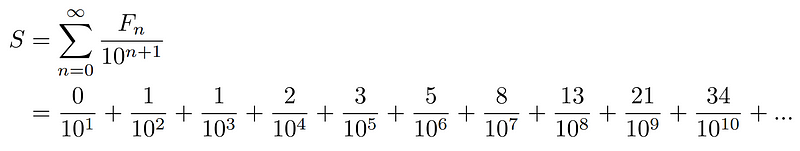
Dividing by 10 yields:
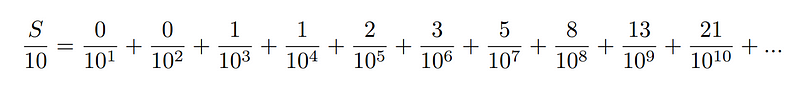
Subtracting the first expression from the second gives:
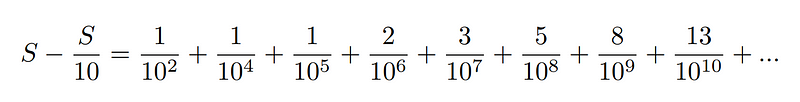
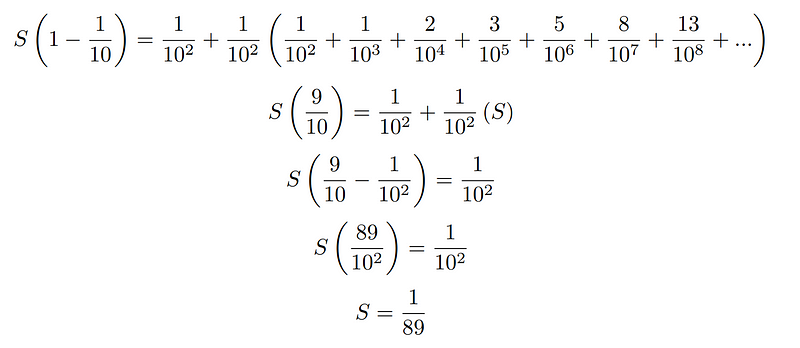
This completes the proof.
Generalizing the Concept
Naturally, a true mathematician may wonder, "How can we generalize this concept to create a more universal expression? What if we want n digits of space for each Fibonacci number?" This leads us to the following formulation:
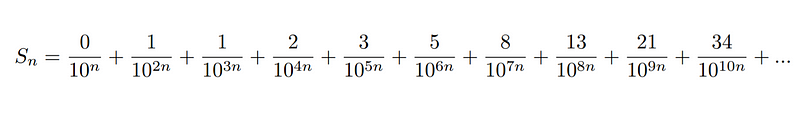

Thus, we have derived an expression capable of generating the Fibonacci sequence as a decimal expansion. Let's put it to the test to confirm its functionality:
Firstly, substituting n=1 yields the earlier result.
Next, testing n=5 provides another clear continuation of the pattern.

Limitations
To maintain fairness, it's essential to discuss the drawbacks of this approach. To accurately determine the nth Fibonacci number, one must assess the size of the number to use the appropriate n value. Otherwise, dealing with overlapping digits can be quite cumbersome.
Benefits
On the upside, this method for calculating the nth Fibonacci number operates at a speed comparable to the fastest known techniques (like Matrix Exponentiation). Moreover, it offers an intriguing way to find Fibonacci numbers, allowing for manual calculations unlike Binet's Formula.
I plan to explore the computational aspects of this formula in a future article. For now, I will conclude this discussion. Farewell.
This video explores the hidden cycles within the Fibonacci sequence, illustrating its connection to mathematics and nature.
In this video, the captivating lore of the Golden Ratio and its relationship with the Fibonacci sequence is explained in detail.