Understanding the Tip of the Cartesian Leaf: A Python Approach
Written on
Introduction to the Cartesian Leaf
In today’s exploration, we delve into the fascinating concept of the Cartesian leaf, named after the illustrious mathematician and philosopher René Descartes. In 1638, Descartes posed a challenge to Pierre de Fermat—the same Fermat known for his famous theorem—regarding how to determine the tangent line at any point on the curve. While Fermat tackled the problem with ease, Descartes found himself stumped. Today, we'll take a different approach by locating the tip of the leaf using a method developed by another notable French mathematician of the same period, Joseph-Louis Lagrange.
The Challenge
The Cartesian leaf is represented by the following equation:
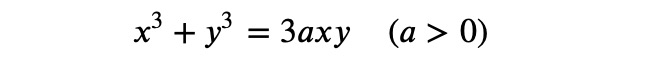
When plotted on a plane (for ?=1), the curve appears as follows:
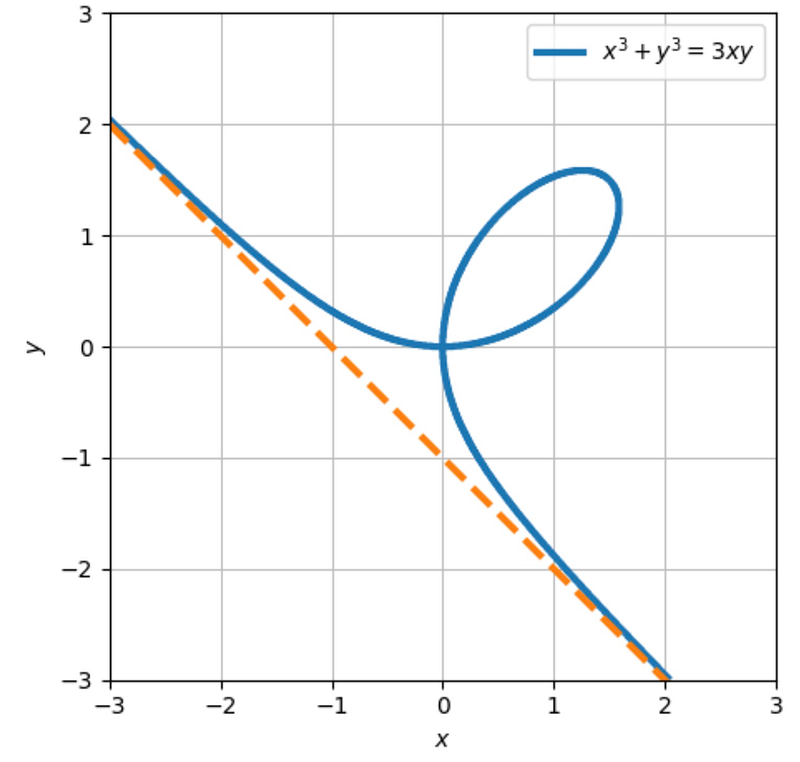
Our goal today is to identify the coordinates of the leaf's tip.
Solving the Problem with Python
To begin, we will use Python's symbolic mathematics library, sympy. We will initiate a Jupyter notebook, define the necessary symbols, and set up the equation for the Cartesian leaf:

So, where exactly is the tip located? The tip can be found at the point where the distance from the origin reaches its maximum. This distance from the origin can be expressed as:
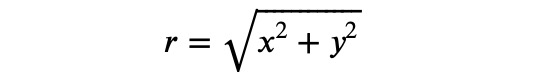
Since maximizing ? also maximizes ?², we can simplify our calculations by avoiding square roots. Thus, we need to ensure that:
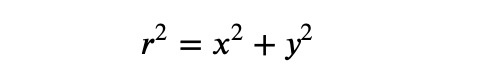
However, this condition must only apply to points that satisfy the Cartesian leaf equation. This scenario leads us to the concept of “Lagrange multipliers,” where we seek to find maxima under constraints.
To apply this, we can rearrange the Cartesian leaf equation into a new function:
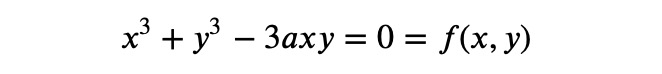
This function is essentially zero, which means that differentiating it with respect to ? or ? will yield zero. Therefore, the total differential can be expressed as:
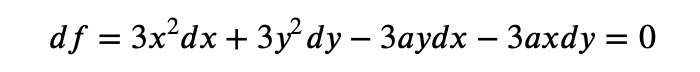
In Python, this can be represented as follows:

We aim to maximize ?², thus we need to satisfy:
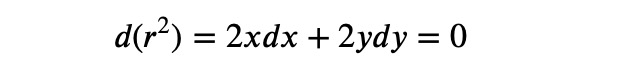
This leads us to the equations ?(?²)=0 and ??=0. Consequently, for some constant ? (referred to as the Lagrange multiplier), we also derive:
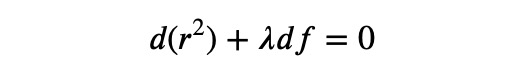
Since both ?² and ? are functions of ? and ?, we equate:
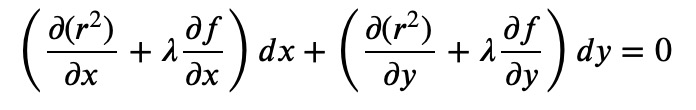
Given that ?? and ?? are variables, this can only hold true if the terms in braces are zero. In Python, this is expressed as:

Next, we will solve the first equation for ? and substitute it into the second equation to eliminate ?:

However, we must also satisfy the original equation for the curve. Thus, we need to solve:

Upon reviewing the output closely, we find that the solution set contains a single real solution, which corresponds to:

This point represents the tip of the Cartesian leaf.
Exploring Further with Video Resources
To enhance your understanding, check out the following videos:
The first video, What is the folium of Descartes? - Week 5 - Lecture 4 - Mooculus - YouTube, provides an insightful overview of the folium concept.
The second video, Folium Descartes x^3 + y^3 - 3xy = 0 Vertical Tangent Implicit Differentiation AP Calculus, delves into implicit differentiation related to the folium.