Chapter 1: Introduction to Spherical Harmonics

Spherical harmonics appear prominently when expanding a Laplacian in spherical coordinates. In this section, we will derive these functions.

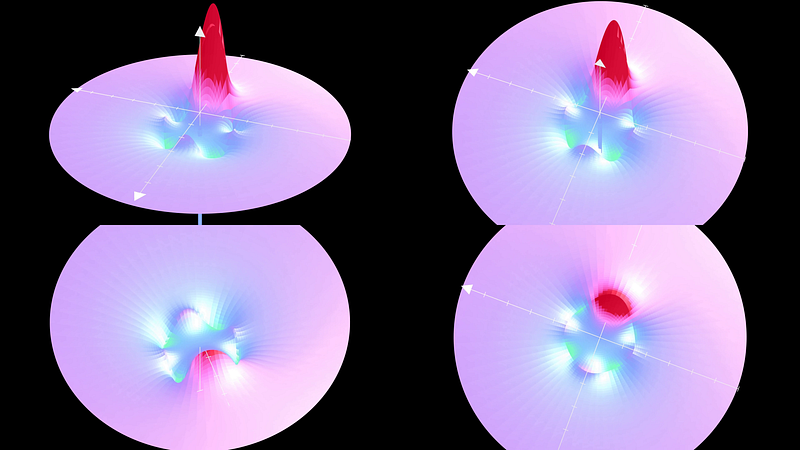
This article is part five of a series titled "The Road to Quantum Mechanics." The potential is observed from four distinct perspectives. The upper two images depict various angles, while the lower left shows the underside and the lower right presents a top-down view of the potential.

Having covered topics such as coordinates, Newtonian Mechanics, Partial Differential Equations in Classical Mechanics, and Fourier Series, you might be wondering when we'll delve into Quantum Mechanics. To satisfy your curiosity, I encourage you to consult someone knowledgeable in Quantum Mechanics and ask them if the concepts discussed here will be relevant to Quantum Mechanics. After they confirm this, please return to continue reading.

Don't look up how spherical harmonics are applied in Quantum Mechanics just yet, as it may cloud your appreciation of the material presented here. If you are already familiar, avoid introducing any misleading intuitions from Quantum Mechanics.

Check Your Understanding

In this section, you will derive some key functions utilized in physics. Even if you struggle with the problems, attempt to formulate incorrect answers and explain their flaws. Problems marked with asterisks are more challenging.

Hermite Equation

Resolve the following equation using the series method.

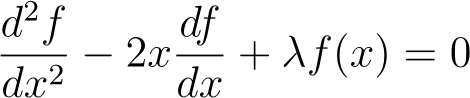
The outcome will be a linear combination of Hermite polynomials.

Helmholtz Equation*

Solve the Helmholtz Equation in spherical coordinates.

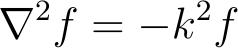
The radial component will resemble the Bessel Equation, which requires the Frobenius method for resolution. Rather than the series solution discussed earlier, you will propose a series solution of the form

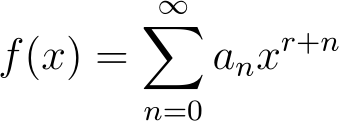
where r is a parameter. You can refer to the video below for a comprehensive example.

Laplace’s Equation in Spherical Coordinates

The Laplacian in spherical coordinates is represented as follows:

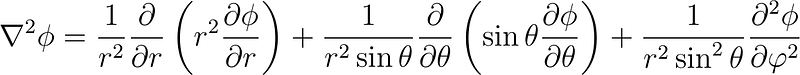
As you might deduce from this expression and the exercises in the "Check Your Understanding" section, this article will delve deeply into mathematical concepts. Let's proceed.

The Radial Equation

Similar to the previous article, we will assume our function can be expressed as a product of two functions of different variables, R(r) and Y(?, ?). The functions Y(?, ?) are identified as spherical harmonics. We will substitute ?(r, ?, ?) = R(r) Y(?, ?) into the differential equation

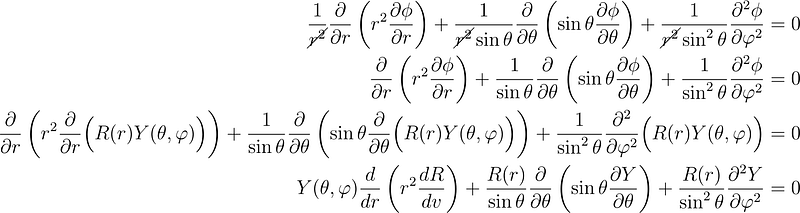
and rearrange to isolate all r-dependent terms on one side and all ? and ?-dependent terms on the other side.

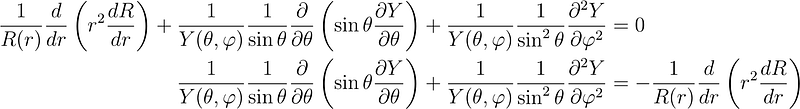
This leads us to conclude that both sides must equal a constant.

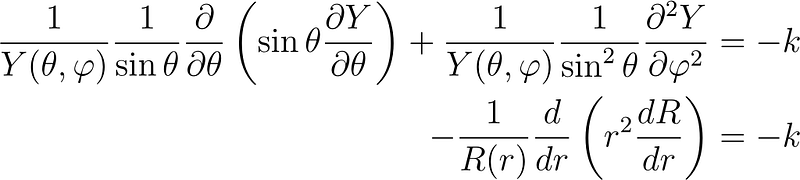
If any part of this process is unclear, revisit the previous article.

First Attempt

We aim to solve the radial differential equation, which is a specific instance of an Euler-Cauchy Equation.

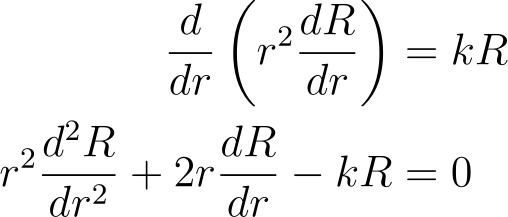
If you've taken a Differential Equations course, your initial guess will likely involve an exponential function. However, attempting this approach yields:

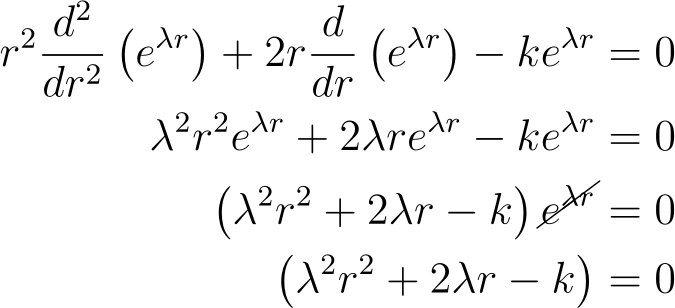
There is no constant ? that satisfies this equation for all r, indicating that the solution cannot be of this form.

Second Attempt

Instead, let's try another expression. Our alternative class of fundamental functions in Calculus consists of polynomials. We will begin by testing the simplest polynomial (a monomial).

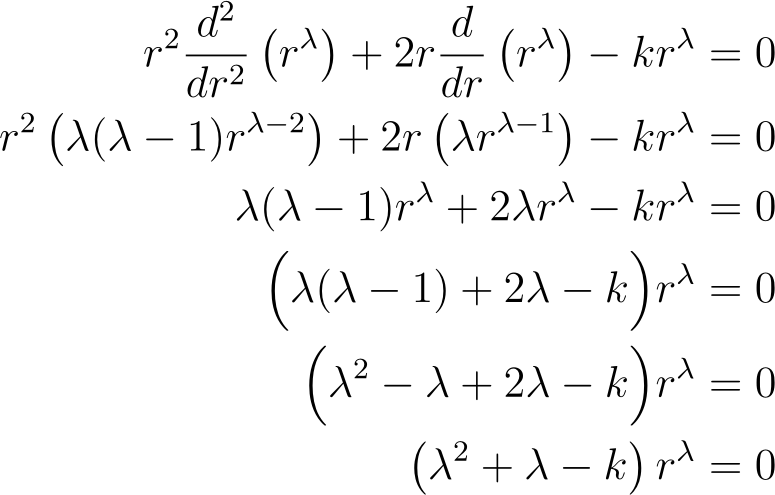
This leads us to either ?² + ? – k = 0 or r = 0. The case r = 0 is valid for only one value, so we focus on ?² + ? – k = 0. From this, we can apply the quadratic formula to solve for ?.

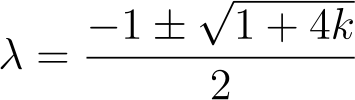
As we will discover later, k must take the form ? (? + 1), simplifying this expression considerably.

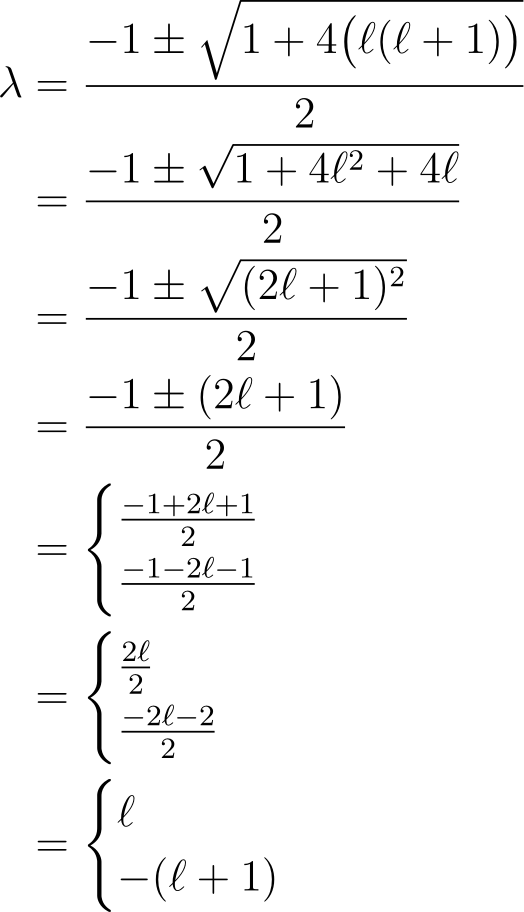
Consequently, our solution for the radial equation is:

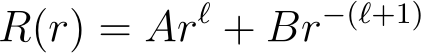
where A and B are constants dependent on ? and another index.

Physical Restrictions

The solution diverges when r = 0 or as r approaches infinity. To maintain finite potentials, we set B = 0 near the origin and A = 0 as we move away from it.

Total Spherical Symmetry

In cases of complete spherical symmetry, all terms except for the ? = 0 term will vanish, leading to our solution:

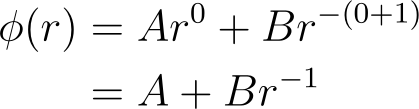
If you recall from Physics II, you've encountered this solution before. If you maintain a spherical shell of radius R at a consistent potential V, the electric field inside the sphere must be zero, implying that the potential remains constant. Beyond the sphere, the potential diminishes as 1/r. Thus, the potential as a function of r is represented as:

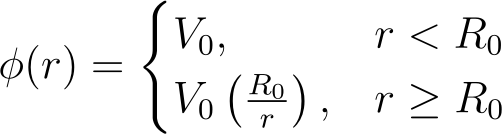
Separating the Angular Components

Next, we will separate the angular components into distinct equations.

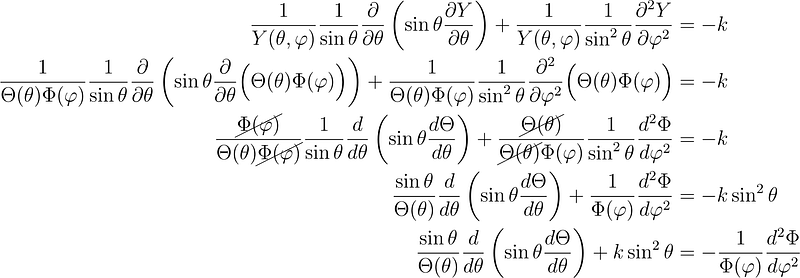
We then equate both sides to a constant.

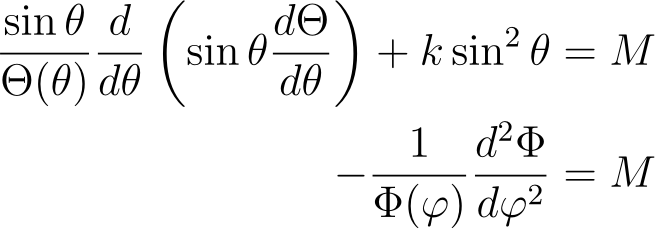
The Azimuth Equation (?)

We can solve the azimuth equation:

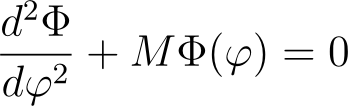
using the standard characteristic equation method, yielding

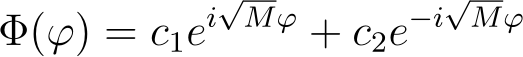
where c? and c? are constants influenced by the eigenvalue M. These constants will eventually be incorporated into the A and B constants from the radial component, but they are retained here for clarity.

Periodicity of ?

We need to impose a condition on the value of M. In spherical coordinates, the azimuthal angle corresponds to longitude. Traveling around a sphere at constant latitude should bring us back to our starting point, implying that the coordinates (r, ?, ?) and (r, ?, ? + 2 ?) refer to the same spatial point. Therefore, for every spatial location, there can only be one value for the potential, leading us to the periodic boundary condition:

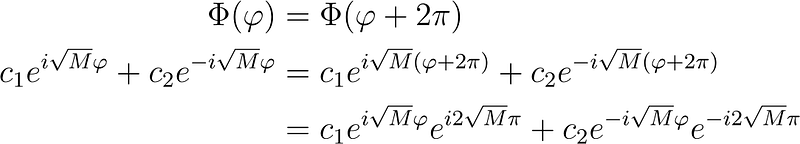
This must hold for all values of c? and c? if

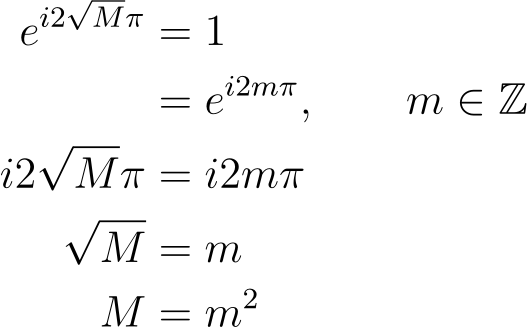
Ultimately, we conclude that M = m², where m is an integer.

The Zenith Equation (?) (The Challenging Part)

I will outline several non-intuitive steps, but the core concept will be to eliminate the trigonometric functions. We will first address the simplest case (m = 0) and then propose a solution in the form of an arbitrary polynomial, extending it to accommodate non-zero m.

Simplifications

Substituting M = m² into our zenith equation yields:

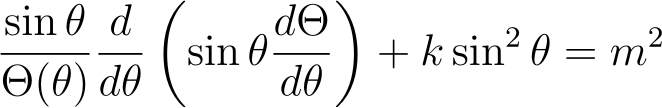
We can expand it to reduce the number of trigonometric terms.

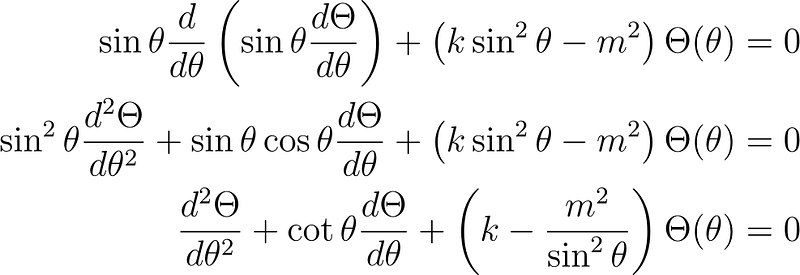
We can eliminate the trigonometric functions by assuming a function of the form ?(?) = P(cos ?). We will first need to find d?/d? and d²?/d?².

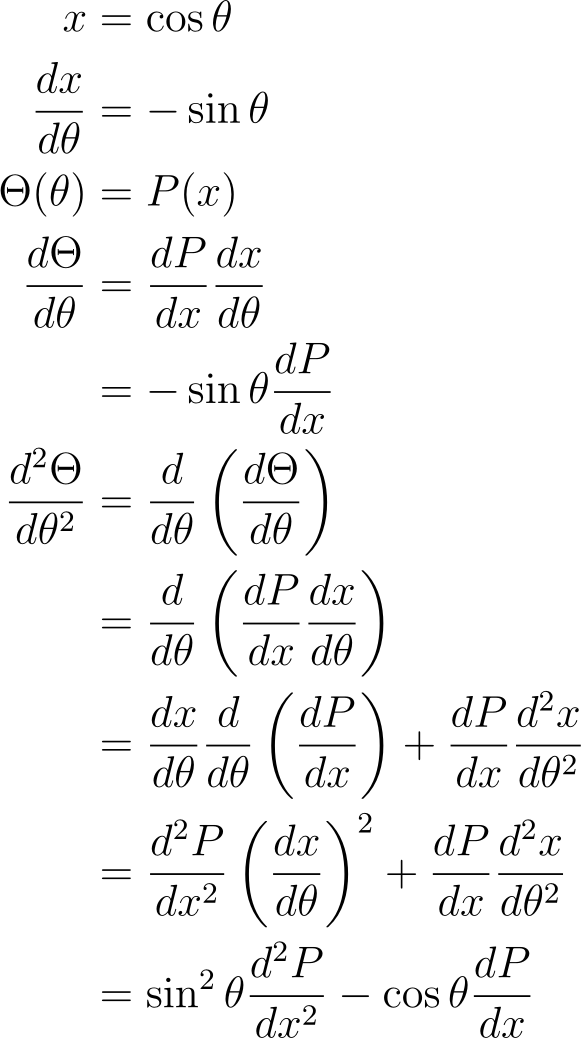
Substituting this result into the zenith equation gives us:

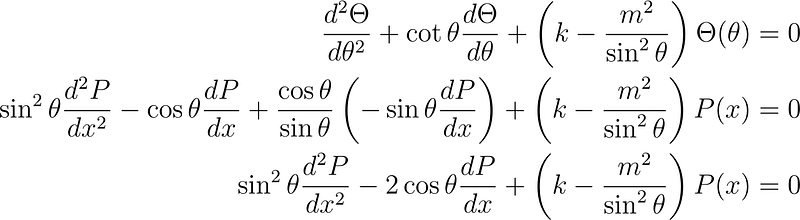
By making the substitutions x = cos ? and sin² ? = 1 – cos² ? = 1 – x², we can eliminate all trigonometric terms.

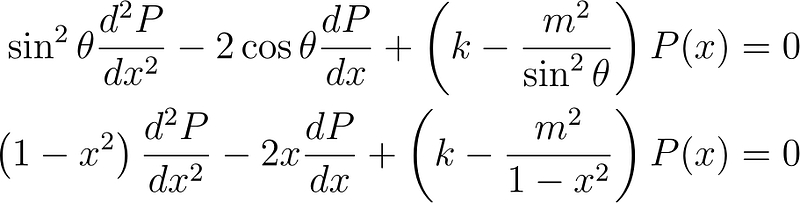
This equation is recognized as the Associated Legendre Equation.

Let m = 0

Setting m = 0 leads us to the Legendre Equation:

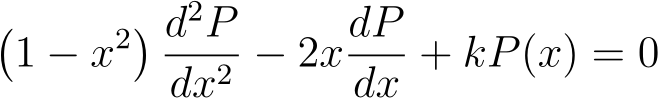
We will first resolve the Legendre equation and then leverage its solution to tackle the associated Legendre equation.

Series Solution

You might hypothesize that the solution is an exponential or a power of x. Neither will suffice, so we will solve this equation using a series approach. We will assume the solution can be represented by a polynomial of arbitrary degree:

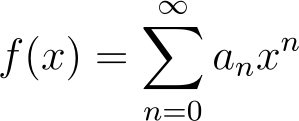
For finite-degree polynomials, all coefficients beyond a certain point must be zero. For instance, to represent 2 x³ – 10 x² + 1, we would have:

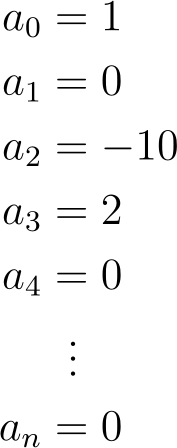
Example

Let's attempt to solve a simpler differential equation prior to addressing the Legendre Equation.

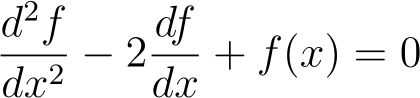
First, we substitute our series and apply standard derivative rules.

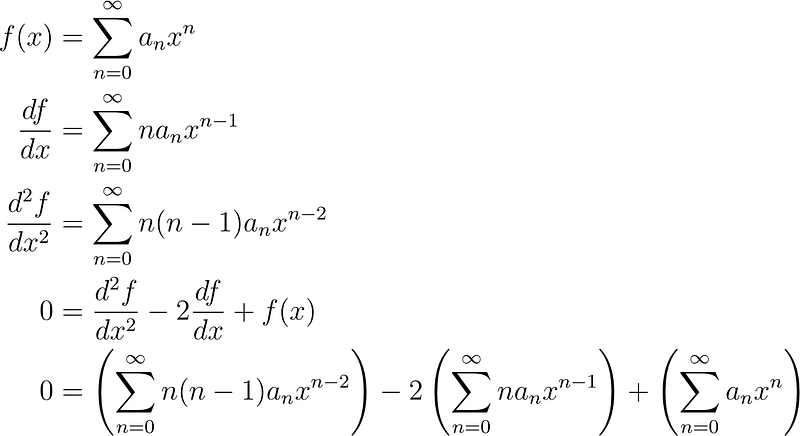
The summation is useful for abstracting much of the complex work, yet we should investigate the underlying details. Writing out the initial terms yields:

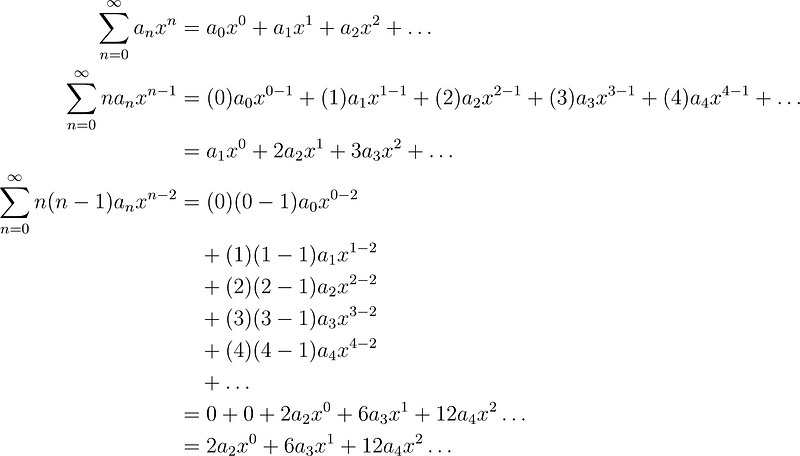
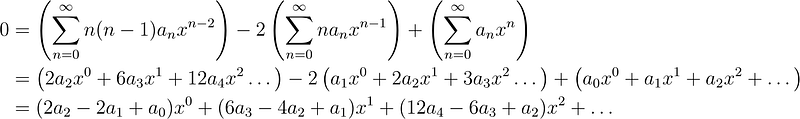
As observed, we arrive at another series. For this series to equal zero for all x, all coefficients must also be zero. To simplify, we may revert to the sum format and re-index everything.

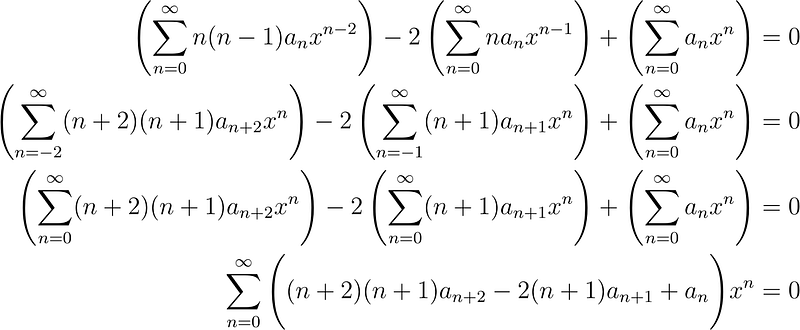
Transitioning from line one to line two, I allowed n ? (n + 2) in the first sum and n ? (n + 1) in the second sum. This adjustment changes the lower bound from n = 0 to n + 2 = 0, altering its lower bound to n = –2. Similarly, the lower bound in the second sum shifts to n = –1. Moving from line two to line three, I recognized that the n = –2 and n = –1 terms of the first sum and the n = –1 term of the second sum were zero, allowing me to disregard them by setting both lower bounds to n = 0. The final line results from grouping and factoring all terms. Consequently, all coefficients must be zero for this solution to hold for every x, which leads us to:

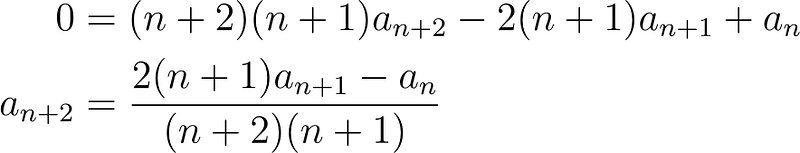
This sequence of coefficients is termed a recurrence relation. There are no restrictions on a? or a?, yet every subsequent coefficient is determined by a? and a?. For second-order linear ordinary differential equations, we anticipate two constants. In this scenario, those constants are a? and a?.

Just Polynomials?

To clarify, this method can address problems where the solution may not seem polynomial in nature. Our series solution above corresponds to

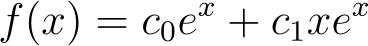
which can be verified by expanding the Taylor series at x = 0. This solution can also be derived using the characteristic polynomial method. Finding a closed-form expression for an arbitrary sequence can be complex and often infeasible; however, there are methods beyond the scope of this article.

Series Solution to the Legendre Equation

Returning to the Legendre Equation, we will employ the same process. First, we calculate the derivatives.

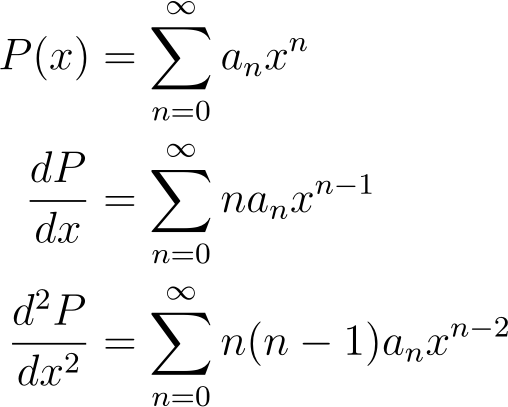
Next, we substitute these results into the equation and consolidate everything.

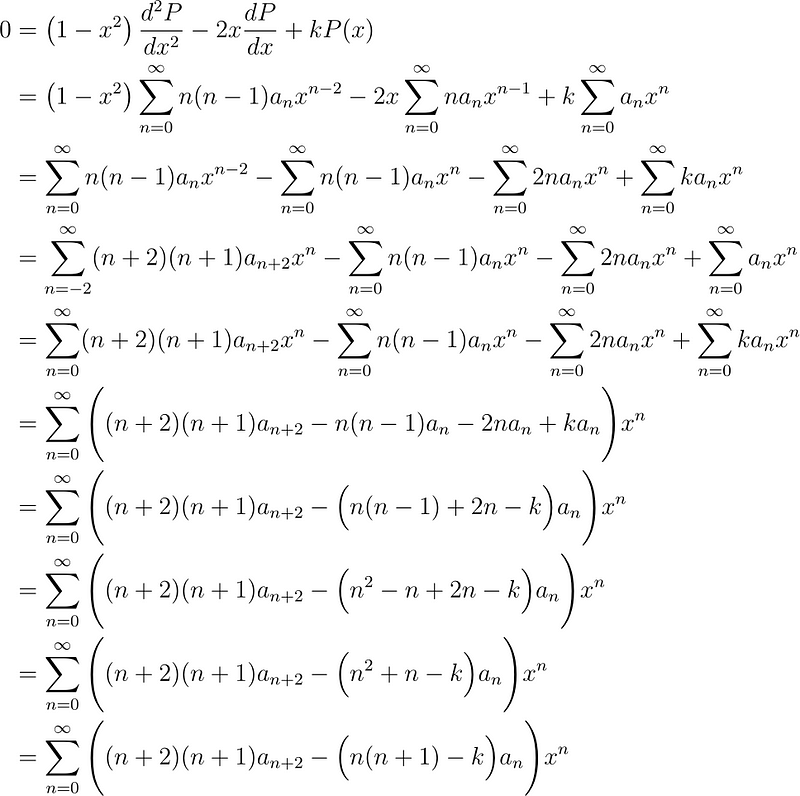
Setting the coefficients to zero leads to a new recurrence relation.

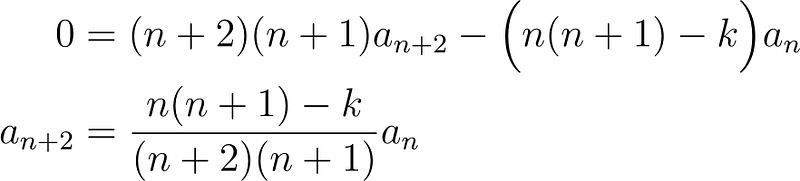
This relation allows a? and a? to vary freely.

Restrictions on k

We aim to substitute cos ? for x, limiting our considerations to the interval x ? [-1, 1]. At x = 1 and -1, the series will diverge unless all coefficients beyond a certain point are zero. The divergence at the top (? = 0) and bottom (? = ?) of a sphere results in infinite potential, leading to numerous complications, as the "top" and "bottom" of a sphere are arbitrary. To resolve this issue, we must ensure all coefficients beyond a certain point are zero. We can achieve this by examining the recurrence relation closely.

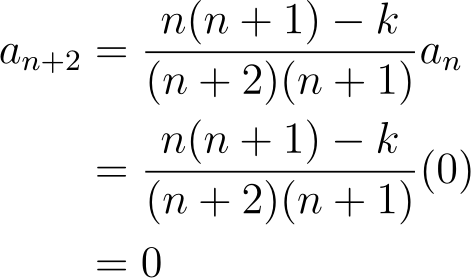
If the a? coefficient is zero, then the a??? term must also be zero. By induction, we can assert:

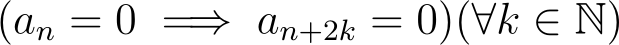
This result indicates that by nullifying a coefficient, we can eliminate either all even or all odd coefficients that follow. If we do not start with a? = 0 or a? = 0, a value of n exists where a? ? 0 but a??? = 0. At this value, denoted as ?, we have:

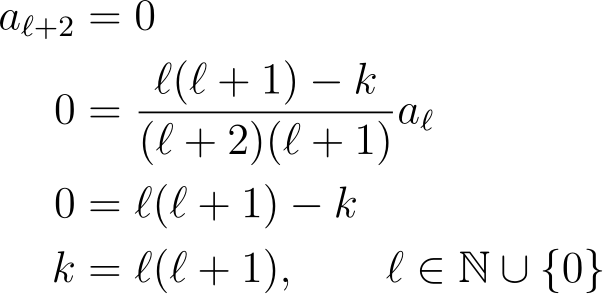
To ensure that all even or odd terms beyond a certain point are zero, we set k to ? (? + 1), where ? is a non-negative integer. This also allows us to express the recurrence relation neatly.

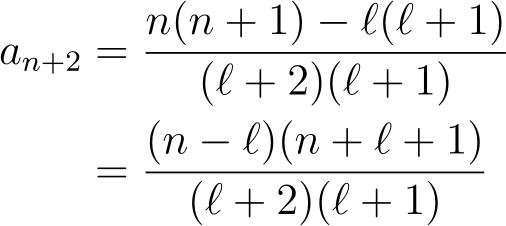
If we choose ? as an even non-negative integer, all even terms after n = ? will equal zero, but the odd terms will remain non-zero. We can nullify them by setting a? = 0. Conversely, if ? is an odd non-negative integer, we can make the even terms zero by setting a? = 0. By leveraging the linearity of the Legendre Equation, we can express the physical solution as a linear combination of the solutions we have derived.

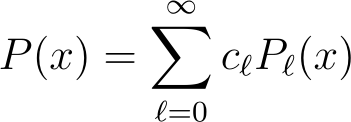
The P?(x) functions are known as the Legendre Polynomials. The first few Legendre Polynomials are:

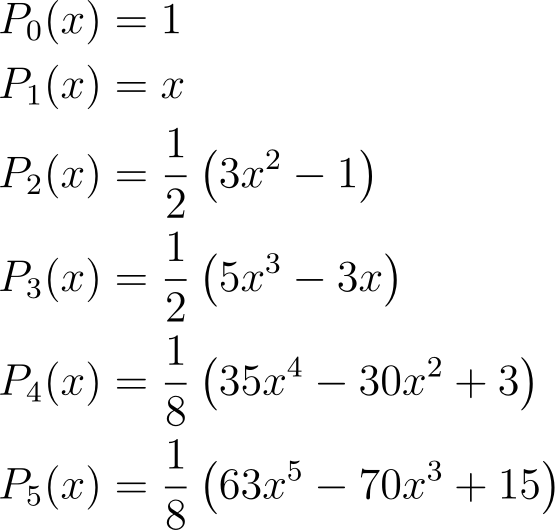
These have been normalized to ensure that P?(1) = 1.

Can You Really Just Ignore Half the Terms?

The Legendre Functions of the Second Kind (which we disregarded by setting a? = 0 or a? = 0) always tend to infinity at -1 and 1, making them irrelevant in this context.

What About Negative ??

We can also truncate the series at a certain point n = –(? + 1) with ? = –(n + 1). The results will yield the same outcomes as when ? = n, indicating that negative values of ? do not contribute additional solutions.

Let m ? 0

Most sources will follow the pattern we established, then state, "When m ? 0, the solution is … Moving on." However, we will formulate a guess for the solution's structure and proceed from there. We will define the associated Legendre polynomials as the functions that satisfy the associated Legendre equation:

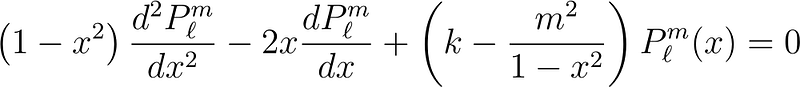
When m = 0, these associated Legendre polynomials reduce to the Legendre polynomials.

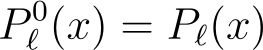
To generate a suitable guess, we must consider the general solution to the Laplace equation.

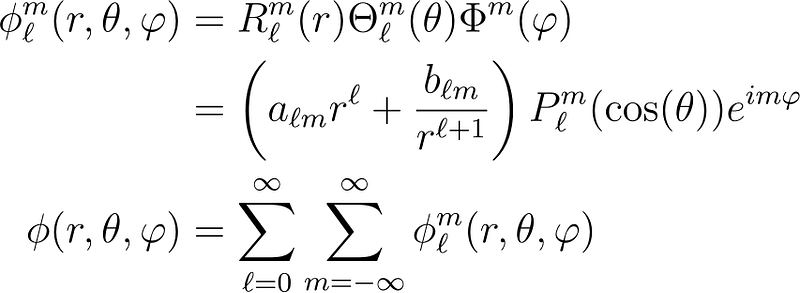
When examining the coordinates (r, 0, ?), specifically for m = 0, we get:

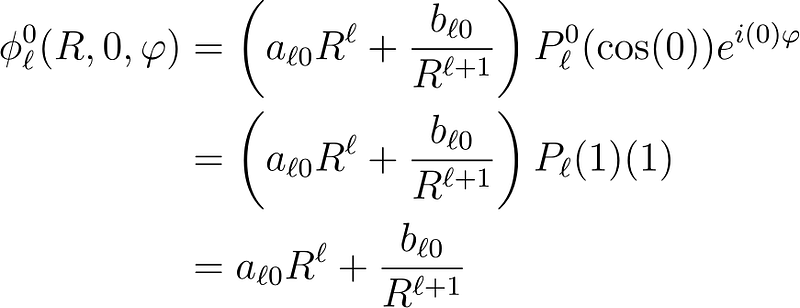
This remains valid. Conversely, when m ? 0, we obtain:

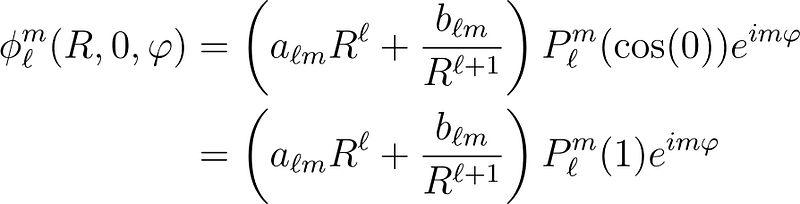
This situation presents a conflict. The coordinates (R, 0, ?) and (R, 0, ?) both indicate the same spatial point (the top of the sphere), but our ??m(R, 0, ?) will yield different values due to the ?m(?) term. To resolve this issue, we must accept that either m = 0 or ??m(0) = P?m(1) = 0. Similarly, we can assert that either m = 0 or ?(?) = P?m(-1) = 0, as (r, ?, a) and (r, ?, b) also refer to the same point in space (the bottom of the sphere). Our first condition when m ? 0 is ?(0) = ?(?) = 0, leading to a solution of the form:

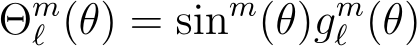
Although the exponent m may seem unconventional, I have yet to find a comprehensive explanation, aside from the notion that "it simply works." It aligns with the mathematics, suggesting that m = 0 necessitates the exponent be zero, so I will proceed with this assumption.

Why not sin(m ?)?

Both forms are roughly equivalent; however, the chosen form simplifies our calculations.

The Chebyshev polynomials relate cos(nx) to cos^n(x). There may also be an argument stemming from Sturm-Liouville Theory, which we will discuss in a subsequent article.

Back to the Equation

We begin by calculating the terms involved in the associated Legendre equation.

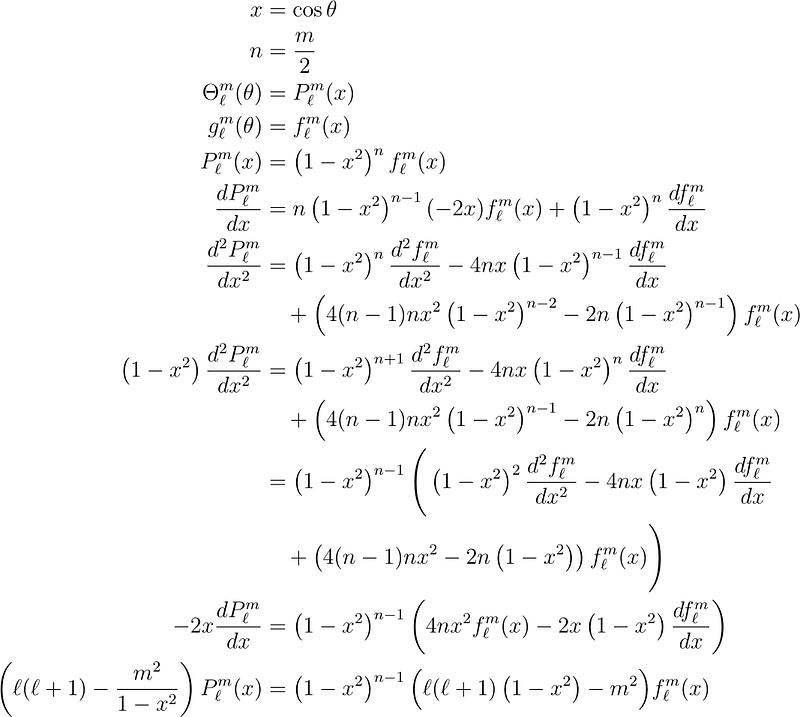
Substituting these into the associated Legendre equation gives us:

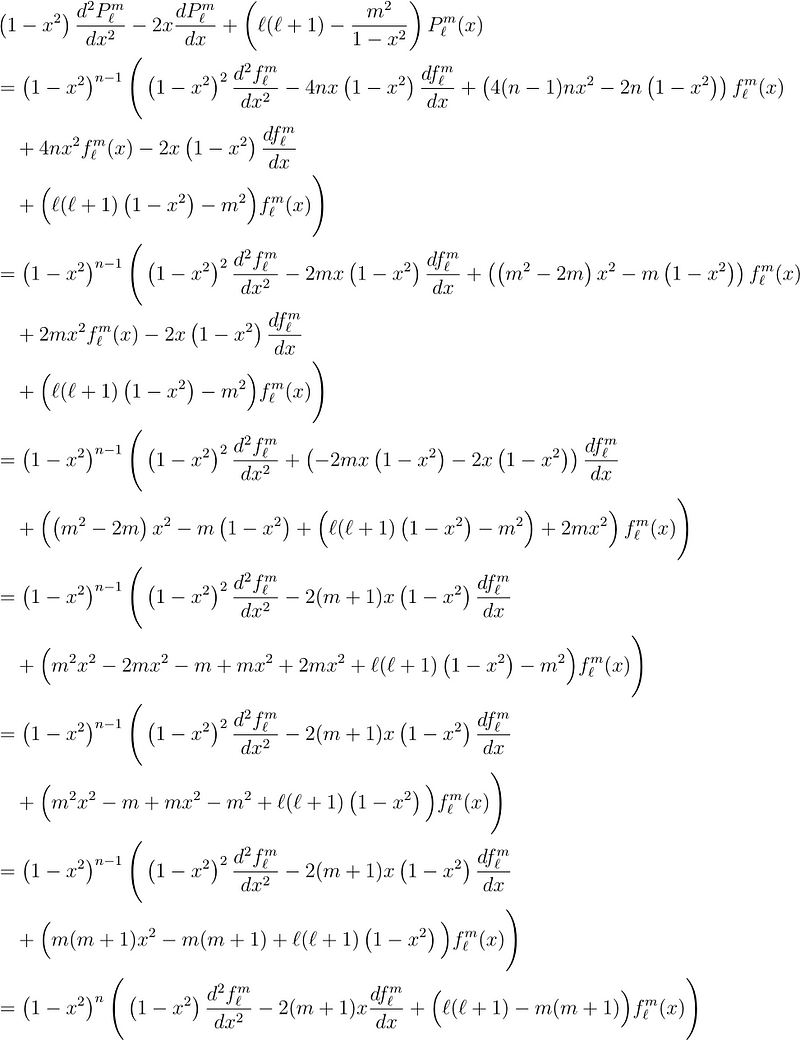
This equation equates to the associated Legendre equation, thus equals zero. We may disregard the outer term since it only holds true for x = ±1, leading us to:

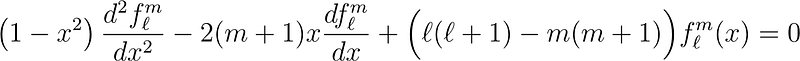
Setting m = 0 recovers the Legendre Equation. Taking the derivative of this equation results in:

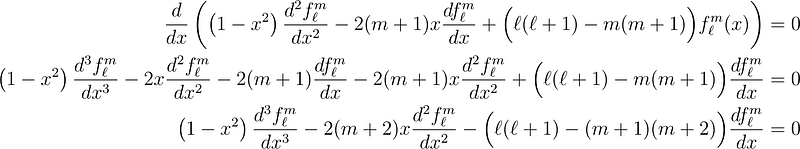
This indicates that if we possess a function that resolves the equation for m = k, its derivative will satisfy the equation for m = k + 1. Mathematically, we express this as:

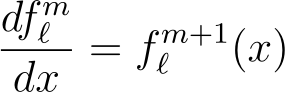
Since m = 0 provides the Legendre equation, we ascertain that:

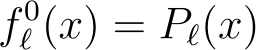
To acquire the function for m ? 0, we differentiate m times.

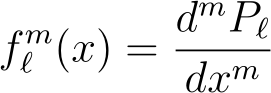
In conclusion, we substitute our findings into our proposed P?m(x).

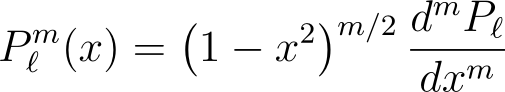
These functions are known as the associated Legendre polynomials. Since the Legendre polynomials are defined to have degree ?, we can only differentiate them ? times. This means m must be less than or equal to ?. This restriction does not lead to any loss of generality.

What About Negative m?

As only the square of m appears in the associated Legendre Equation, the solution for positive m applies equally to negative m. To maintain consistency with certain recurrence relations, the negative m solutions are scaled versions of the positive m solutions.

The Full Solution to Laplace’s Equation in Spherical Coordinates

The general solution is:

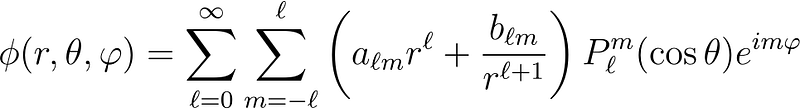
You can verify that this solution satisfies Laplace’s Equation. But how do we determine the coefficients? In the previous article, we employed the inner product. As we are working with complex functions, we will utilize the complex version of the inner product (refer to the exercise in the previous article).

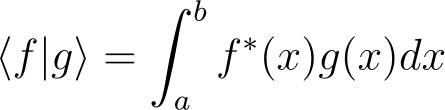
If we attempt to apply this inner product definition to spherical harmonics, we will not achieve orthogonal eigenfunctions. To illustrate why, let's compare the above definition to the inner product of two complex vectors in arbitrary dimensions.

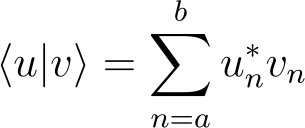
Aligning the components reveals:

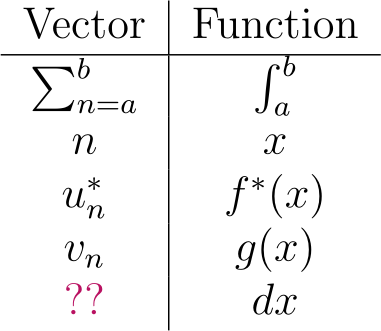
Every aspect of the integral inner product corresponds with the vector inner product, with the exception of the dx term. The dx is somewhat arbitrary, especially when considering u-substitutions. Consequently, the general form of the inner product for two functions over the interval (a, b) is:

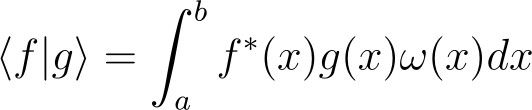
We refer to the function ?(x) as a weight function.

Motion of Particles

We will discuss how to derive weight functions in the subsequent article. For now, I want to provide an idea of what spherical harmonics resemble. Animating a 2D function on a 2D surface embedded in 3D space is challenging (particularly since my animation software lacks the necessary capabilities). To simplify, I chose a potential exhibiting rotational symmetry around the z-axis, ensuring that only the m = 0 terms are non-zero. This allows me to animate a cross-section of the sphere, where the surface height indicates potential, with the highest peak aligning with the negative z-direction. I selected the coefficients:

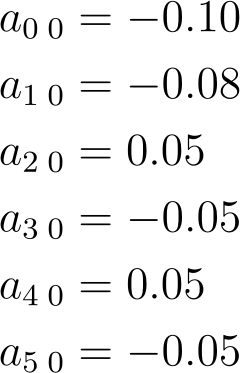
defined at a radius of 1.5, resulting in:

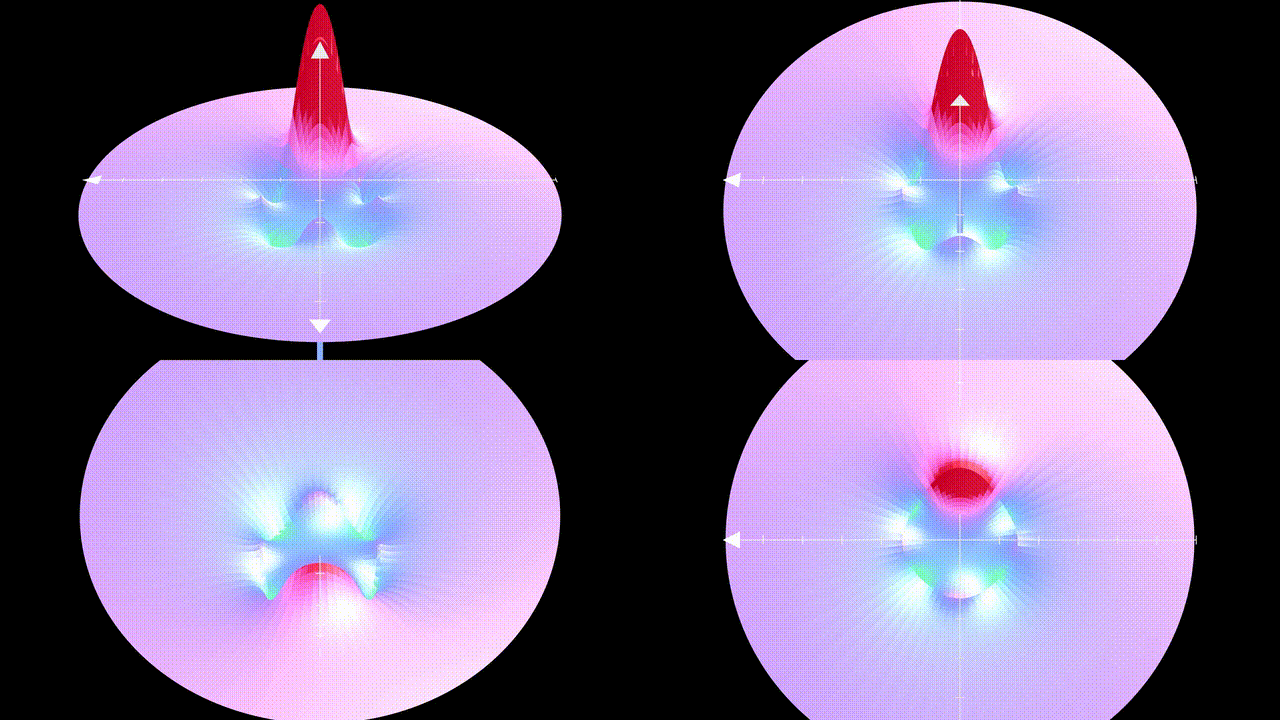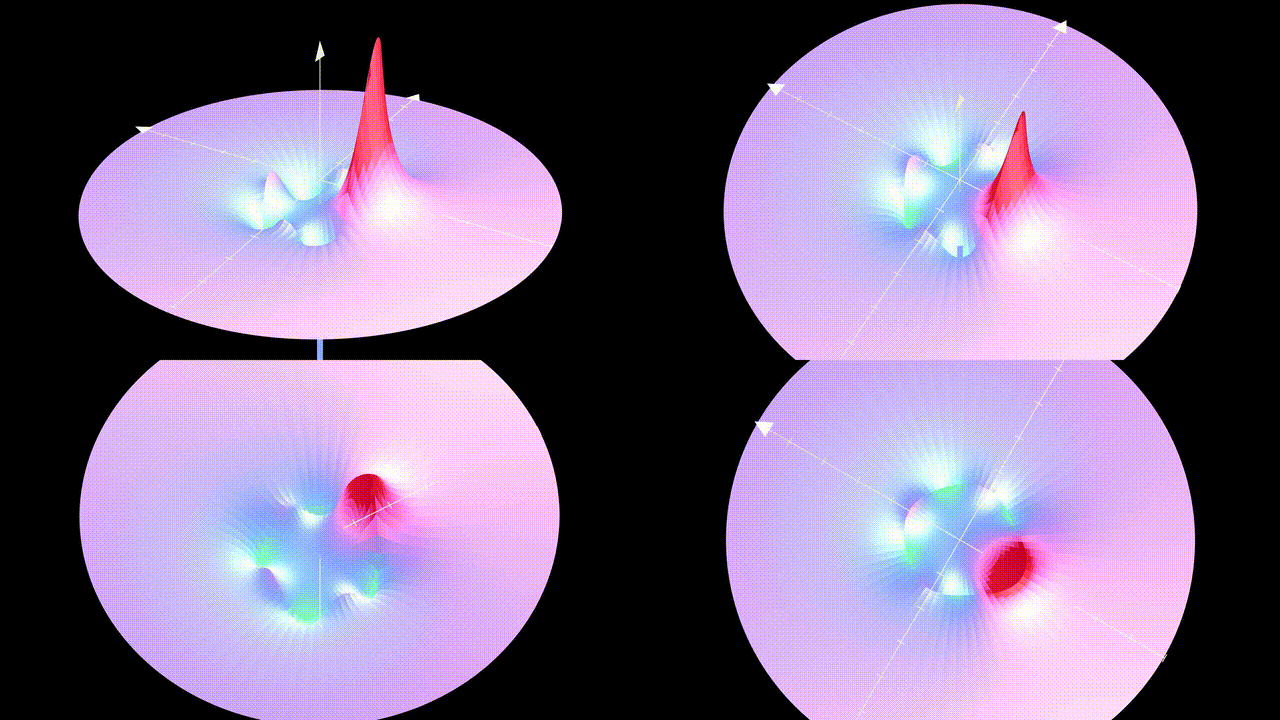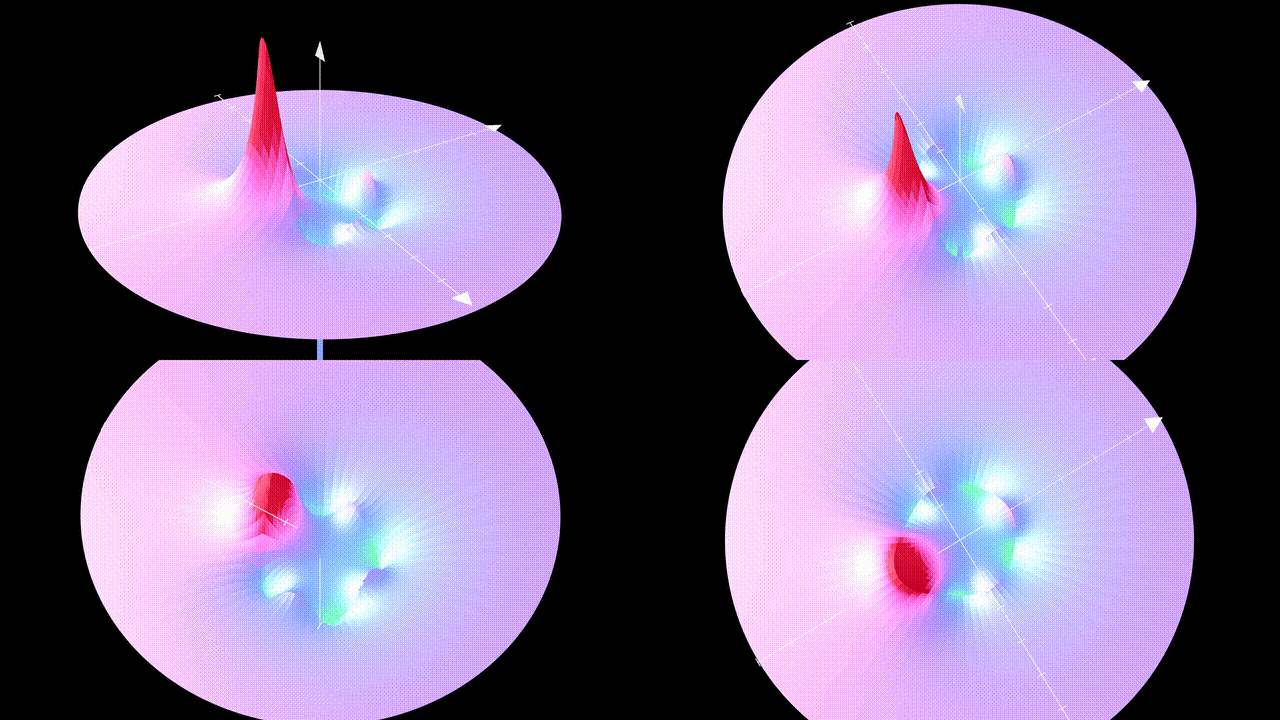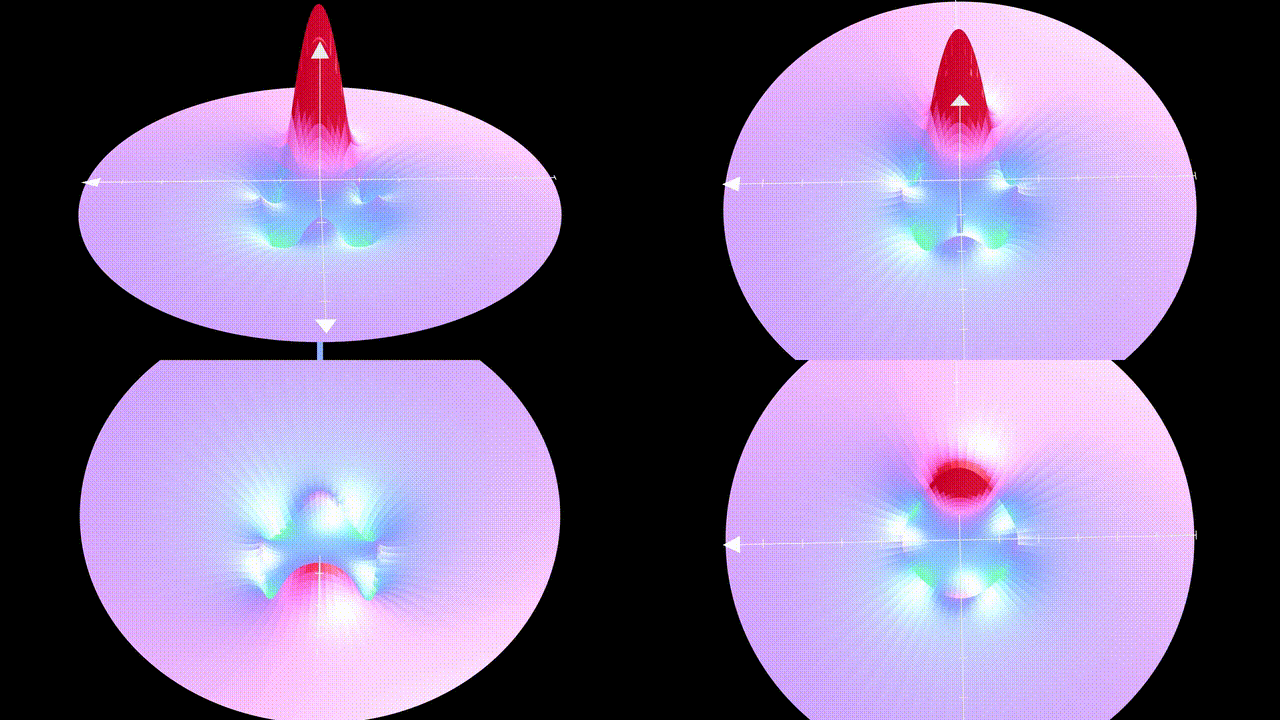
The top two videos present different perspectives. The lower left depicts the underside, while the lower right offers a top-down view of the potential. The circles are visual artifacts resulting from my use of a gif.

I also released test particles into this potential (although crossing through the sphere might not be feasible, as the force may not be defined at the sphere's surface) to demonstrate the outcome.

The dark red circle indicates the sphere's boundary. The sphere's bottom corresponds to the red peak in the previous video.

Launching these particles at a potential not only appears visually striking — it serves as an effective means to deduce an unknown potential or charge distribution.

This contributes to multiple aspects discussed in this article.

A Brief Note About Potential Theory

Potential Theory focuses on harmonic functions, which are solutions to Laplace’s equation. I previously linked a comprehensive textbook in the last article, but there's an intriguing fact evident from the animation above. The maximum principle asserts that the maximum of any non-constant solution to Laplace’s equation can be located on the solution's boundary. In this instance, it is clear that all maxima and minima reside on the sphere that delineates the interior from the exterior.

Summary

In this article, we explored numerous new concepts, including:

• Euler-Cauchy Equations,
• Various constraints on eigenfunctions,
• Series solutions to differential equations,
• The Spherical Harmonics,
• A glimpse into Potential Theory (as an added bonus).

If you've managed to navigate through this article successfully, great job! Give yourself a pat on the back and attempt some exercises in the "Check Your Understanding" section. If you encountered difficulties, please leave a comment, and I’ll assist you.

What’s Next?

I apologize for leaving you on a cliffhanger, but I couldn't justify adding eight more minutes of complex mathematics to derive the weight functions in this article. As I mentioned earlier, I try to stay several articles ahead of my current writing to ensure topics are cohesively arranged and that later articles are consistent with earlier ones. For instance, I began discussing projection operators as part of a later article in a different context. Before completing this article, I realized that projection operators provide essential background for understanding weight functions, prompting me to shift the weight function discussion to the next article alongside projection operators. In explaining projection operators, I recognized the need to clarify bra-ket notation as well. Consequently, the upcoming article will address bra-ket notation, projection operators, Hermitian operators, weight functions, and orthogonality.