Chapter 1: Introduction to Analytic Continuation

Analytic continuation is a pivotal concept in complex analysis that allows us to expand the domain of an analytic function. This technique plays a crucial role in addressing some of the most profound questions in mathematics, such as the Riemann hypothesis, which pertains to the distribution of prime numbers.

Figure by agsandrew/shutterstock.com

Section 1.1.1: Taylor Series

A Taylor series provides a polynomial approximation for a function f(x). Polynomials are expressions formed using variables and coefficients, involving addition, subtraction, and multiplication with non-negative integer exponents. A polynomial of degree n can be expressed as:

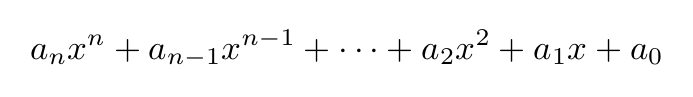
The concept extends to infinite-degree polynomials, known as Taylor series, which represent functions as infinite sums of terms derived from the function's derivatives at a specific point.

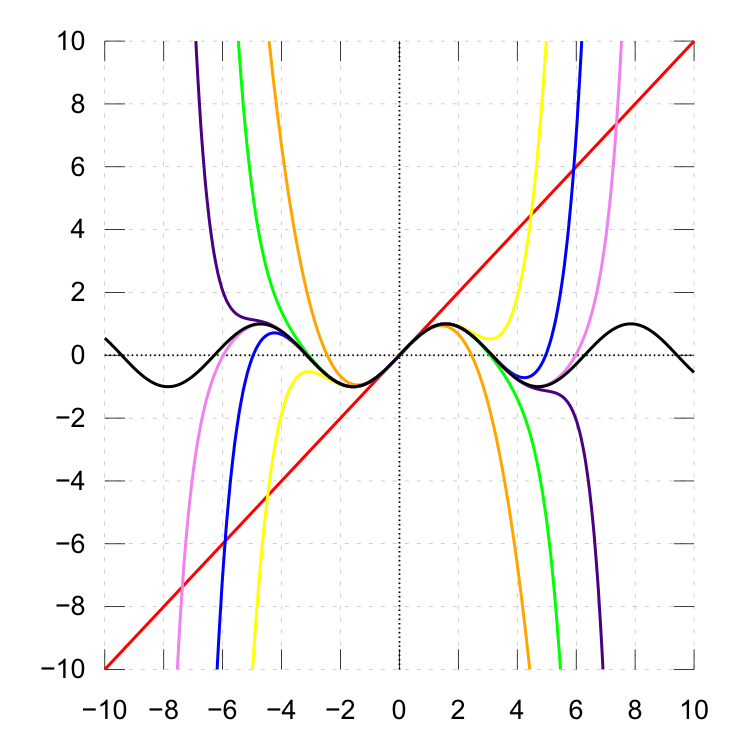
The Taylor polynomials for f(x) = sin x are showcased, illustrating how they converge to the actual function as more terms are added.

Section 1.1.2: Convergence

Understanding convergence is critical when discussing analytic continuation. A sequence is an ordered list of elements, and a series is formed by taking the sum of a sequence.

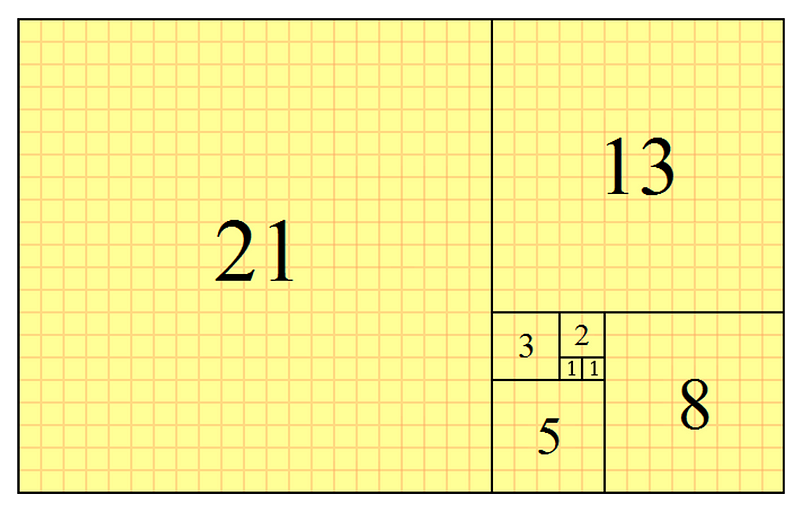
For example, the Fibonacci sequence is a well-known sequence where each number is the sum of the two previous numbers.

A series converges if the sequence of its partial sums approaches a finite limit. Conversely, a series is divergent if it does not converge.

Chapter 2: The Role of Analytic Continuation

The primary function of analytic continuation is to broaden the domain of an analytic function. Formally, if f(z) is analytic in a region R contained within a larger region S, then f(z) can be extended to S through a function g(z), satisfying specific criteria.

This video, "A Gentle Discussion About Analytic Continuation," provides an introductory overview of the concept.

Section 2.1: Practical Example of Analytic Continuation

For instance, consider the function

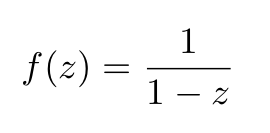
which has a pole at z=1. The convergence disk illustrates where the function behaves well, and we can evaluate derivatives at points within this region.

The video "Complex Analysis: Analytic Continuation" dives deeper into this technique and its applications.

Section 2.2: Application to the Riemann Hypothesis

Georg Friedrich Bernhard Riemann's work on prime numbers heavily utilized analytic continuation. The Riemann zeta function can be analytically continued throughout the complex plane, and the Riemann hypothesis posits that all non-trivial zeros of this function lie on the critical line Re(s) = 1/2.

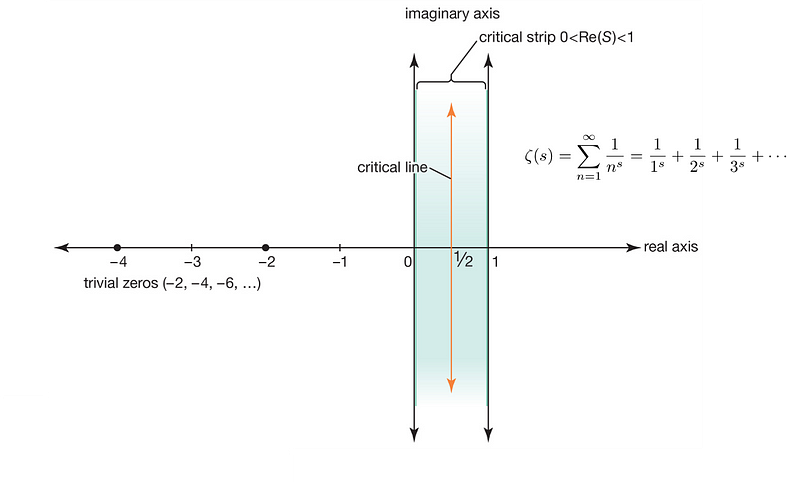
In conclusion, analytic continuation is a powerful tool that extends the reach of analytic functions, with significant implications in both theoretical and applied mathematics.