Convert Between Number Systems Using Logarithmic Methods
Written on
Understanding Number Base Conversion
When converting a number from one base to another, a common approach is utilizing the Euclidean algorithm. This method involves dividing the number by the new base, recording the integer part, and repeating the process until the result is zero. The sequence of remainders derived from this method represents the equivalent value of the number in the new base.
For illustration, applying this algorithm to a specific example results in:
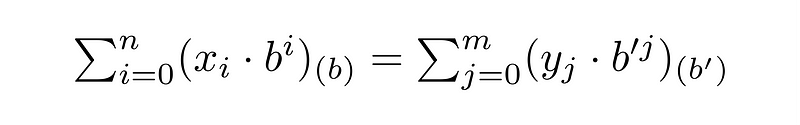
The remainders collected from the calculations yield the binary representation of the original number:
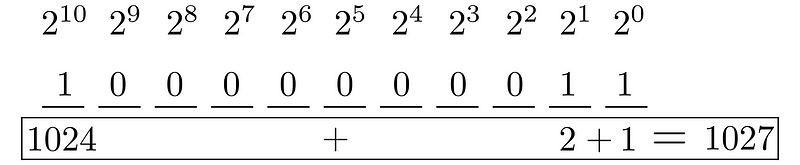
Challenges in Traditional Methods
One significant issue encountered is the presence of consecutive zeros, which cannot be overlooked. The algorithm proceeds smoothly from start to finish without any interruptions. This is where logarithms prove beneficial, as they can simplify calculations by eliminating these zeros.
The key to solving this problem lies in recognizing that if both the result and the base of an exponential function are known, logarithms can be employed to determine the exponent.
Understanding Logarithmic Representation
In modern mathematics, every numeral system is positional. For example, the number 1027 in base 10 signifies:
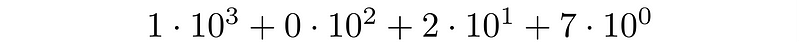
To express this number using logarithms, we identify that the base (10) and the result (1027) are known. This leads to:
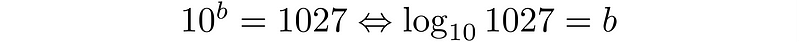
Utilizing a logarithm table or calculator, we find that the exponent, denoted as b, is approximately 3.0115704436. This implies that raising 10 to this power will yield 1027.
To decompose this power, we can separate it into its integer and decimal parts. The integer part, 3, allows us to calculate 10 raised to that exponent, resulting in 1000. This indicates that the digit in the 10³ position is non-zero, specifically equal to the integer part of the subsequent fraction:
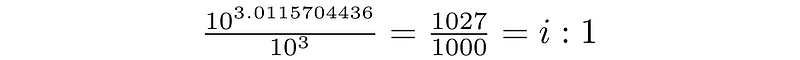
The remainder, shown below,
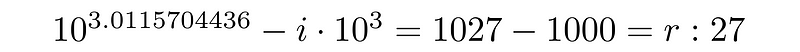
is utilized in the next step, similar to how 1027 was processed earlier.
Converting Between Different Bases
The next phase involves changing the base from 10 to another value, such as 2, 3, or 4. This is achievable due to the properties of logarithms, where the base can be modified without altering the outcome.
Having established the logarithmic principles, we can now analyze whether the following equations hold true:
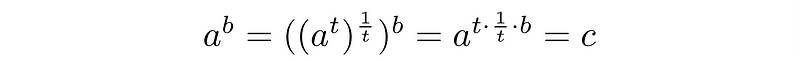
These equations are equivalent because multiplying by the fraction of 1 by t does not affect the exponent.
Now, to shift from one base (a) to another (a’), we need to determine the power to which a must be raised to yield a’. Logarithms provide the answer to this query!
The current equation can be expressed as follows:
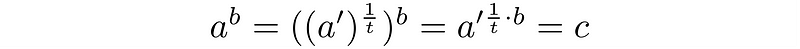
Here, we know b and the fraction, allowing us to derive a new formula for calculating the same c with an alternate base:
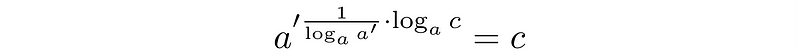
Practical Examples
To convert 1027 from base 10 to binary, we begin by determining t to get a’, which is 2 (the binary system).
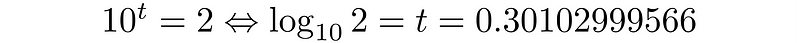
Knowing the value of t allows us to find the fraction quickly:
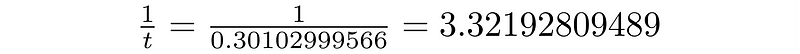
With all constants in hand, we can initiate the algorithm.
First iteration:
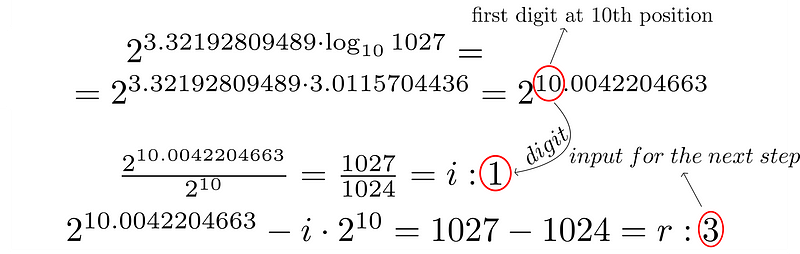
In the binary system, the integer part will consistently be 1. We will calculate each time for a clearer understanding.
Second iteration:

Notice how all zeros have been eliminated; it’s quite remarkable.
Third iteration:
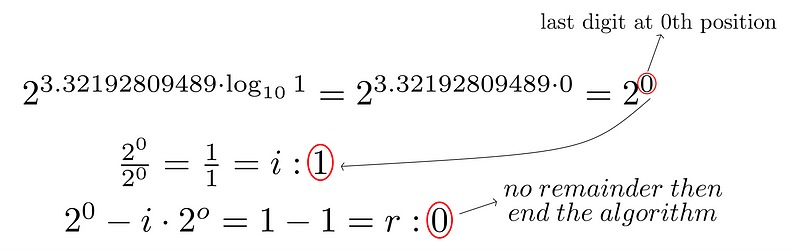
The final outcome indicates that 1s occupy the 10th, 1st, and 0th positions, while all others are 0. We can verify this with the same method as before using a table:
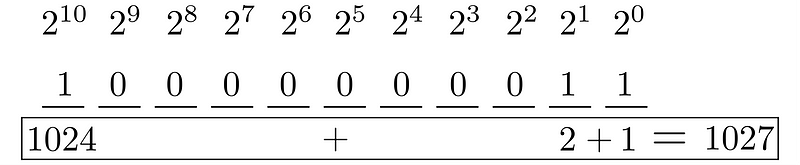
As a more complex example, let’s convert the number 94842243 into the base 3 numeral system.
First, we calculate t to get a’:
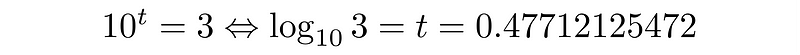
And find the fraction:
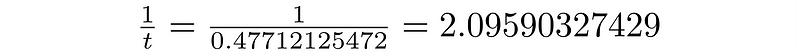
We will now proceed with the iterations, verifying the outcomes as we go.
Final results:

A verification test confirms our results:
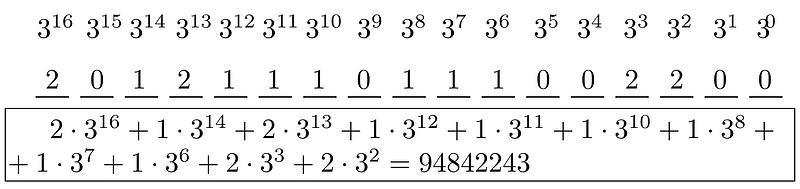
In summary, this process illustrates how to effectively convert numbers between different numeral systems by leveraging logarithms.
The first video provides a detailed explanation on using a multiplication algorithm to facilitate number system conversions.
The second video serves as a refresher on converting between any two number systems, reinforcing the concepts discussed.