# Unraveling the Universe: The Role of Amplituhedron in Physics
Written on
Understanding the Universe's Foundations
For centuries, the fundamental principles of our universe have been a topic of debate among scientists. Despite extensive discussions, a consensus remains elusive. The Large Hadron Collider (LHC) in Switzerland stands as a beacon of hope for physicists seeking answers. This powerful machine accelerates elementary particles, specifically protons, to velocities nearing that of light, subsequently forcing them into direct collisions. These interactions yield images capturing the immediate aftermath, presenting a challenge for physicists in terms of interpretation.
Feynman Diagrams: A Simplified Approach
In the mid-20th century, Richard Feynman revolutionized the analysis of particle collisions by introducing diagrams that simplified complex equations. Feynman's contributions earned him the Nobel Prize in Physics in 1965. However, analyzing collisions at the LHC involves grappling with hundreds of these diagrams. The term "scattering amplitudes" refers to the probability of one set of particles transforming into another upon collision. Feynman's diagrams visually represented all possible scattering scenarios, allowing for a summation of their likelihoods.
The interpretation of LHC collision images relies heavily on computational technology. While mathematical equations can describe the outcomes, solving them demands significant computational resources.
Enter the Amplituhedron
Professor Nima Arkani-Hamed from Princeton University proposes a transformative approach that leverages mathematical constructs to streamline the solution-finding process for these collision equations. One such construct is the 'amplituhedron,' which encapsulates the information of over 200 Feynman diagrams.
NAH's journey to discovering the amplituhedron stemmed from years of contemplation on the limitations of current physics models. His 2013 paper, co-authored with Jaroslav Trnka, ignited discussions within the academic community and hinted at a potential new paradigm in physics. Despite the passage of time, the conversation surrounding the amplituhedron has largely remained within scholarly circles.
This innovative concept links elementary particle collisions to geometric volumes in a theoretical space, resonating with Plato's Theory of Forms, where abstract forms represent the truest reality. Thus, the amplituhedron bridges modern physics and ancient philosophical ideas.
Mathematical Foundations of the Amplituhedron
The discovery of the amplituhedron necessitates the integration of various mathematical and physical concepts. Firstly, it is defined within Anti-de Sitter (AdS) space. Secondly, it employs Grassmannians, a mathematical framework found in numerous geometry branches. The Grassmannian set G(k, V) consists of all k-dimensional linear subspaces in V. Specifically, the amplituhedron exists in the positive Grassmannian. Lastly, it draws upon Twistor Theory, proposed by Roger Penrose in 1967, suggesting that twistor space should be fundamental to understanding physics and the emergence of space-time.
Through substantial effort, NAH postulated the multidimensional nature of the amplituhedron as an abstract entity in AdS space. Its dimensions—length, width, and height—encapsulate information about colliding particles, while the equation governing its volume describes the emerging particles. The following figure illustrates an example of an amplituhedron, resembling a polyhedron formed from various polyhedral shapes.
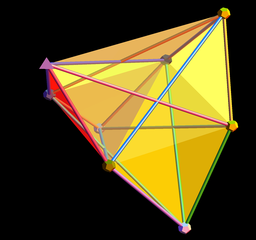
Interpreting Collisions through Geometry
According to NAH, the interactions of virtual particles in our universe can be interpreted as geometric shapes in AdS space. This perspective aligns with the notion that events within our universe can be described as occurrences on the boundary of AdS space, where the bulk consists of polyhedral forms. Consequently, the results of proton collisions can be viewed as mathematical computations.
NAH posits that the discovery of the amplituhedron could lead to a paradigm shift, where space and time are no longer seen as fundamental aspects of nature, but instead understood through the lens of pure geometry, potentially unraveling the mysteries of the Big Bang and the universe's cosmological evolution.
Is the Amplituhedron Merely Mathematical?
In his quest to comprehend particle collisions, NAH conceptualized the amplituhedron as a representation of the events, akin to a map of reality that suggests geometry may underlie the fundamental fabric of the universe. The relationship between the amplituhedron and elementary particles is reciprocal, with each influencing the other.
The intriguing question arises: can our brains be modeled through mathematics?
Chapter 1: The Quest for Understanding
The complexities of particle physics have captivated scientists for generations.
Section 1.1: The Role of the LHC
The LHC accelerates protons, leading to vital discoveries.
Subsection 1.1.1: Feynman's Revolutionary Diagrams
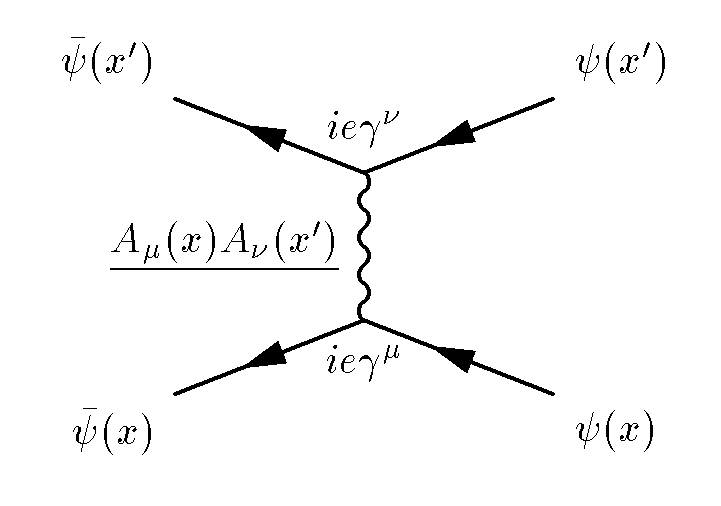
Section 1.2: The Amplituhedron's Significance
The discovery of the amplituhedron offers new insights into particle physics.
Chapter 2: From Geometry to Reality
Explore how geometry shapes our understanding of the universe and the implications for future research in physics.