Chapter 1: Connected Plane Graphs

Connected plane graphs are fascinating structures that consist of vertices and edges, arranged in a two-dimensional space. These graphs are characterized by the property that no edges intersect, resulting in a clean and clear representation of connections between points. The graphs depicted in the illustrations below exemplify connected plane graphs, where you can traverse from one vertex to another solely by following the edges.

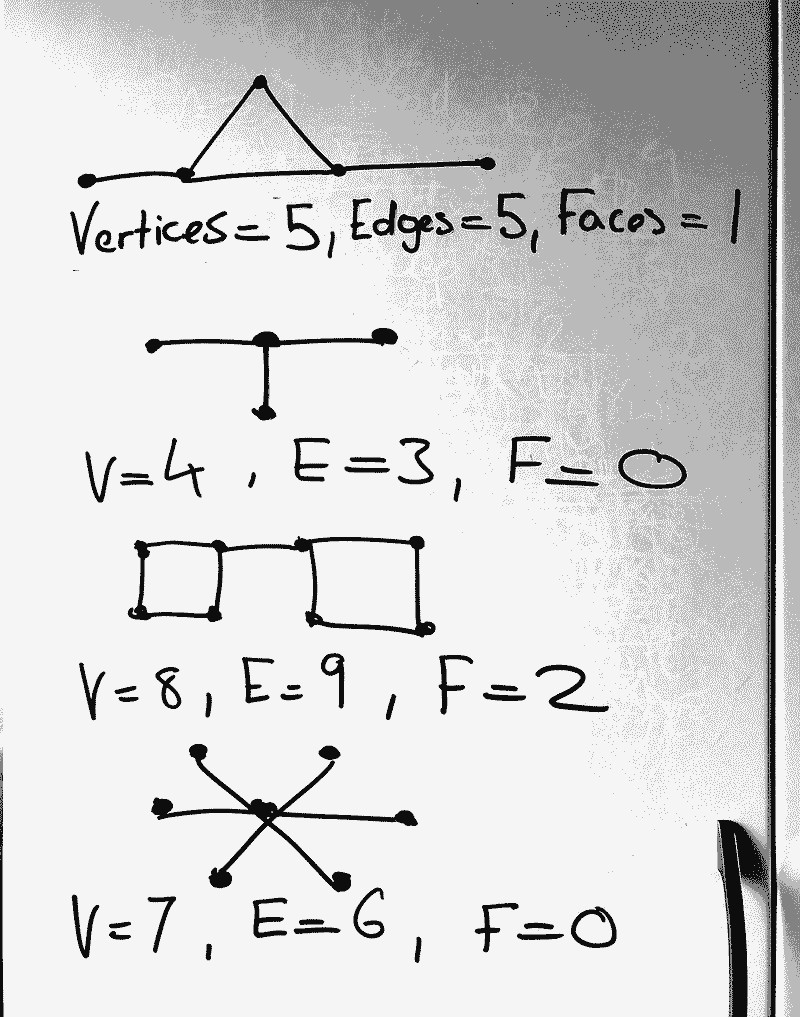
A striking feature of these graphs is the consistent outcome of the equation V - E + F = 1. This relationship holds for every connected plane graph, and it can be demonstrated through a straightforward proof. In fact, it's impossible to construct a connected plane graph that does not satisfy this equation. I encourage you to try creating one yourself!

To establish the validity of this equation, we employ a method known as mathematical induction. The process involves two primary steps: proving that the statement is true for an initial positive integer, and then showing that if it holds for an integer k, it must also hold for k+1.

Let’s define our statement P(k) as V - E + F = 1 for any connected plane graph with k edges, V vertices, and F faces.

First, we confirm P(1) is valid, as the simplest graph consists of 2 vertices and 1 edge, resulting in 0 faces. The equation holds true: 2 - 1 + 0 = 1.

Assuming P(k) is accurate, we now aim to validate P(k+1). A connected plane graph with k+1 edges will either contain a face or not.

If it contains at least one face, we can remove an edge from that face, resulting in a new graph with k edges, V vertices, and F - 1 faces. Since we assume P(k) is correct, we can apply the formula:

V - k + (F - 1) = 1

Rearranging this gives us:

V - (k + 1) + F = 1,

which matches the formula we need for P(k + 1).

In cases where the graph lacks a face, it will possess an end vertex—one connected to an edge on only one side. By removing this vertex and its edge, we create a new graph with V - 1 vertices, k edges, and 0 faces. Again applying P(k):

(V - 1) - k + 0 = 1

Rearranging yields:

V - (k + 1) + 0 = 1,

thus confirming P(k + 1) is true even for graphs with no faces.

This proof elegantly demonstrates that V - E + F = 1 applies universally to all connected plane graphs!

The first video titled "Euler's Characteristic Formula for Planar Graphs" delves into the details of this fascinating mathematical concept, providing visual and theoretical insights into its significance.

Chapter 2: Deeper Insights into Euler's Formula

The implications of Euler's formula extend beyond two-dimensional graphs and offer insights into three-dimensional shapes as well. For those interested in a more comprehensive exploration, the following video sheds light on proving Euler's formula for polyhedra.

The second video, "Proof of Euler's Formula for Polyhedron | Used since childhood, but ever tried to prove?", takes viewers through the reasoning behind this essential mathematical theorem.