Chapter 1: The Basics of Factorials

Factorials can seem daunting at first glance, but they hold incredible power in mathematics. For instance, consider the factorial of 21, represented as 21! = 51,090,942,171,709,440,000.

Images by Author

It's important to recognize that exponential functions outpace polynomial functions. Think about how 2^x grows compared to x²; after x = 2, the exponential function dramatically overtakes the polynomial curve.

However, did you know that factorials grow even faster than exponentials? Take a moment to plot some of these functions to witness their behavior.

With that said, tackling the question of how many odd divisors 21! has can be a fun challenge. I encourage you to pause here, grab a pen and paper, and attempt to solve it yourself before continuing for the answer!

Solution

Our primary method involves examining the prime factorization of 21!. Specifically, we need to determine the total count of 2s in its prime factorization.

Let's delve deeper into this concept.

We utilize Legendre’s formula to find the maximum exponent of a prime number p that divides n!. In our scenario, we repeatedly divide 21 by increasing powers of 2 and sum the integer parts of the results.

This process effectively counts how many multiples of each power of 2 exist within 21, thereby revealing how many factors of 2 are present in 21!.

The powers we consider are:

2 = 2¹, 4 = 2², 8 = 2³, 16 = 2⁴.

By extracting all factors of 2 from 21!, we can conclude that all remaining prime factors must be odd.

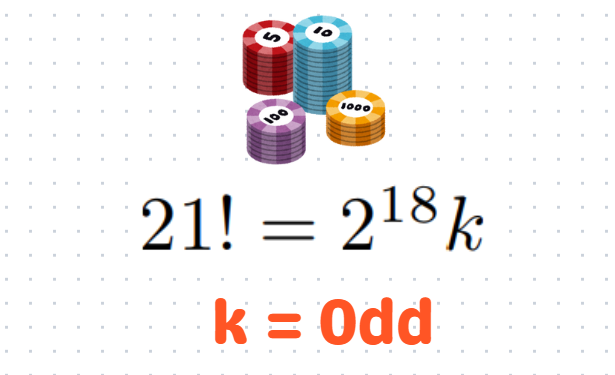
From this, we can deduce that a divisor of 21! takes the form 2^i * b, where 0 ≤ i ≤ 18 and b represents a divisor of k.

For each selection of b, there exists one odd divisor of 21!, accompanied by 18 even divisors. Here, b is the odd divisor while 2¹, … , 2¹⁸ are the 18 even divisors.

Consequently, the probability that a randomly selected divisor is odd is 1/19.

And that leads us to our conclusion.

But wait! Here’s a bonus challenge for you: how many odd divisors does 21! actually possess?

Photo by Milo Weiler on Unsplash

Isn't this fascinating?

What were your thoughts during this process? Please share your insights in the comments; I'm eager to hear from you!