# Mathematical Insights into the Euler-Lagrange Equations
Written on
Chapter 1: Introduction to Variational Principles
In this discussion, I aim to present a more mathematical perspective on the Euler-Lagrange equations. This exploration will start with a review of elementary equations of motion, leading us to the Lagrangian framework.
Section 1.1: Classical Mechanics Foundations
To understand our approach to quantum field theory, we begin by revisiting some fundamental concepts from classical mechanics. The simple harmonic oscillator serves as an excellent example. In classical mechanics, we typically express the motion of a particle ( x ) as a function of time, denoted as ( x = x(t) ). From our high school physics lessons, we know that Newton's laws establish that the product of mass and acceleration equals the force acting on the particle in a single dimension. Therefore, for the simple harmonic oscillator, we can express the equation of motion as follows.
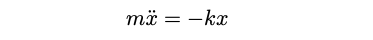
In this equation, ( k ) represents the spring constant. As we progressed through our undergraduate studies, we learned that this scenario is a specific instance of a particle's motion within a potential ( V ), where for a simple harmonic oscillator, ( V(x) = frac{1}{2} k x^2 ). The governing equations of motion can then be expressed in the following form, where the nabla operator indicates the first derivative of the potential concerning spatial variables.
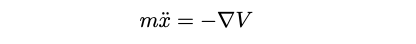
Section 1.2: The Lagrangian Framework
To derive the equations of motion, we can utilize the principle of least action. This principle posits that a particle will follow a path that minimizes the integral of the Lagrangian over time. In practical terms, to determine the particle's path between two specific points in time, ( t_1 ) and ( t_2 ), we aim to minimize the action, represented as ( S ).
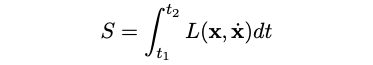
We impose a condition that the endpoints are fixed, such that ( x(t_1) = x_1 ) and ( x(t_2) = x_2 ). To minimize the action, we introduce a small variation in the position, denoted ( x rightarrow x + delta x ). This adjustment also affects the velocity of ( x ). By applying the chain rule to the variables ( x ) and its velocity, we arrive at the following expression, where the delta preceding ( S ) indicates a small change in the action.
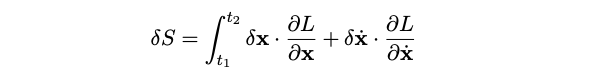
We can integrate by parts on the second term by shifting the variation from ( delta x ) to the integrand. This integration by parts results in a surface term that can be set to zero, given our earlier stipulation that the path does not vary at the fixed points ( x_1 ) and ( x_2 ).
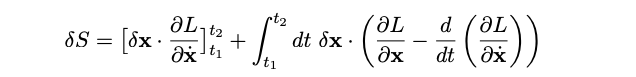
What is the significance of this derivation? Because our variation was arbitrary, the integrand must equal zero for any change in ( x ). This leads us to the conclusion that the term in brackets must vanish, which is precisely the Euler-Lagrange equation. This method provides a straightforward way to derive the equations of motion for any Lagrangian, and I will discuss its applications in various fields in a subsequent post.
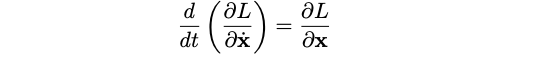
Chapter 2: Exploring Video Resources
This first video, titled "Derivation of the Euler-Lagrange Equation | Calculus of Variations," provides a comprehensive look at deriving the Euler-Lagrange equation using calculus of variations.
In the second video, "Introduction to Variational Calculus - Deriving the Euler-Lagrange Equation," the presenter offers a thorough introduction to variational calculus and its applications in deriving the Euler-Lagrange equation.