Mastering Integration by Parts in Calculus: A Comprehensive Guide
Written on
Chapter 1: Introduction to Integration Techniques
In this section, we delve into a specific problem encountered in the 18.01 Practice Final exam from Fall 2003. The question at hand involves solving a challenging integral.
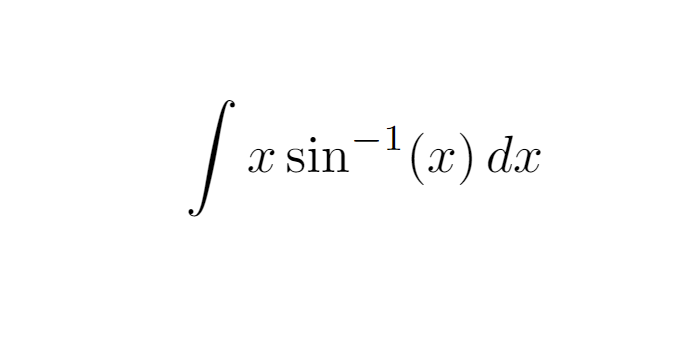
When faced with an integrand that consists of the product of two functions, a widely-used approach is integration by parts.
Section 1.1: Understanding Integration by Parts
The essence of this technique lies in selecting ( u ) as the function that is easier to differentiate and ( dv ) as the function that is simpler to integrate. In this particular scenario, we will designate ( u ) as the inverse sine function and ( dv ) as ( x , dx ).
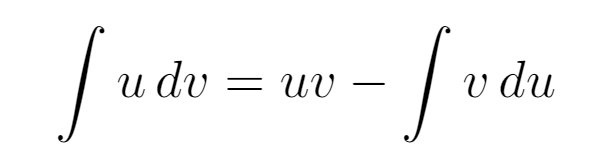
Now that we have established both the derivative of ( u ) and the antiderivative of ( dv ), we can substitute them into the integration by parts formula.
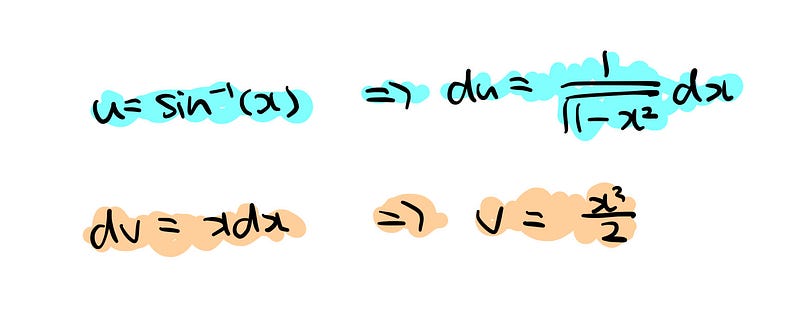
Notice how the integration by parts technique simplifies our problem? Initially, we were tasked with finding the antiderivative of the inverse sine function, but now we only need to deal with a more manageable integrand on the right.
To resolve the integral on the right, we can employ a trigonometric substitution.
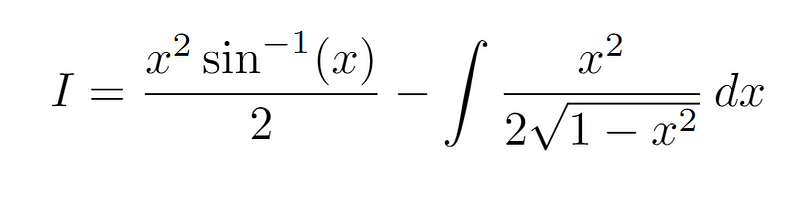
We will set ( x = sin(u) ).
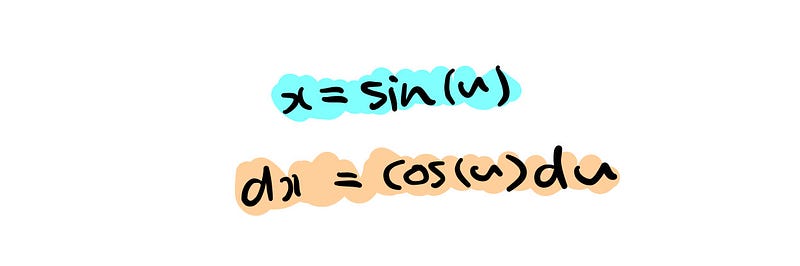
We can further refine the integral on the right by utilizing the Pythagorean identity.
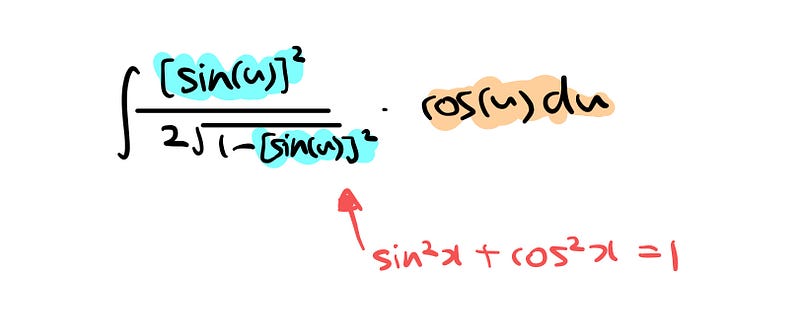
The denominator transforms into ( 2sqrt{cos^2(u)} ), leading us to the expression above. Remember this fundamental trigonometric relationship?
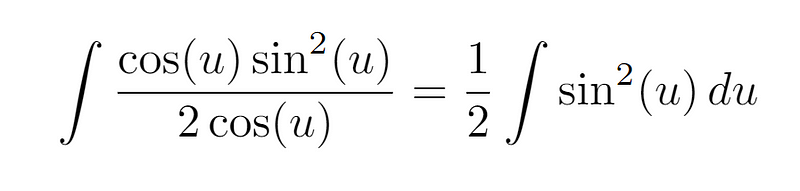
The integral we are working to compute becomes further simplified.
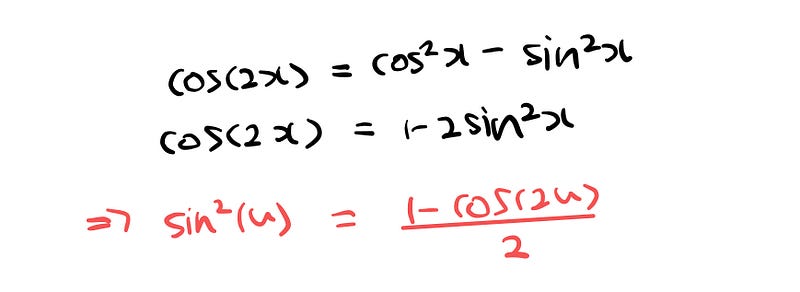
After performing the integration, we arrive at the following expression.
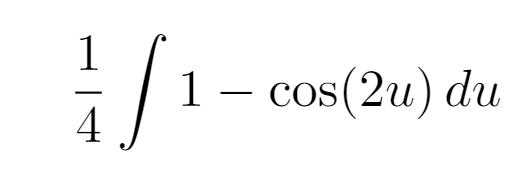
Before substituting ( u ) back into our original equation, we must determine how ( sin(2u) ) relates to ( x ).
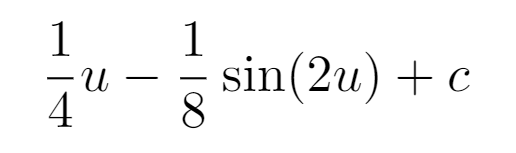
Hopefully, this clarification helps in understanding the next steps. Let’s reintegrate all components back into our integral.
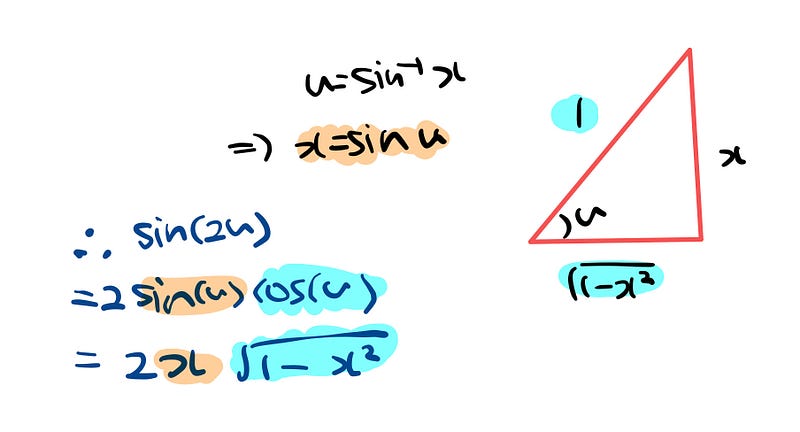
Ultimately, our integral resolves to:
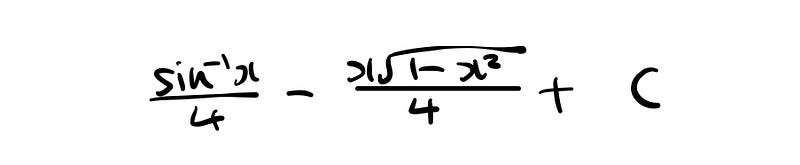
And this serves as a suitable stopping point.
To summarize, we initiated our process with integration by parts by choosing appropriate ( u ) and ( dv ). We then advanced with a trigonometric substitution to simplify our integral, culminating in a right-angled triangle representation to express the integral in terms of ( x ).
And there’s our solution. Isn’t it fascinating?
What thoughts did you have while following this process? Please share your insights in the comments; I’d love to hear from you!
The first video titled "WHAT'S A CALCULUS TEST LIKE AT MIT? | by an MIT student" offers an insider's perspective on the challenges and experiences of taking calculus at a prestigious institution.
Chapter 2: Analyzing Calculus Exams
The second video, "Could You Pass This Harvard University Calculus 1 Final Exam?" poses a thought-provoking challenge for viewers to assess their calculus skills against a real exam.
Thank you for engaging with this material. If you found this information helpful, please consider sharing it with others and expressing your appreciation by clapping for the article.

If you feel inclined, I would greatly appreciate your support through a coffee donation. Your generosity helps sustain my writing and academic pursuits. Thank you!