Chapter 1: Understanding the Infinite Hyperbolic Product

The concept of an infinite hyperbolic product may not originate from a specific competition, yet it employs a technique frequently encountered in various mathematical contests. Let’s delve into the problem at hand:

To aid our understanding, recall the identity:

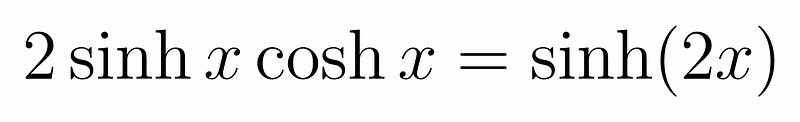
At first glance, this may appear unrelated, but let’s simplify our approach by examining a finite case. Instead of considering an infinite product, let’s evaluate it up to three terms:

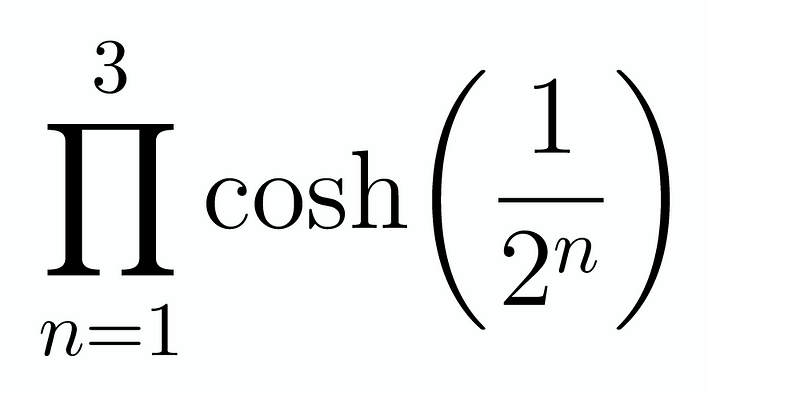
If we multiply the entire product by sinh(1/8)/sinh(1/8), we can express it as:

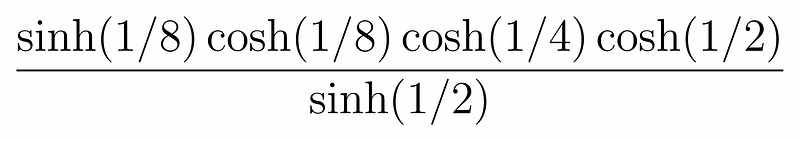
Now, let’s concentrate on the numerator. By applying our previous identity, we can rewrite it as:

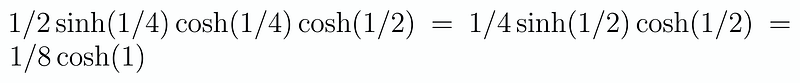
Can you see the direction in which this is heading? However, there remains a challenge: our product is infinite. How do we resolve this? We will explore that shortly. We can express our product as:

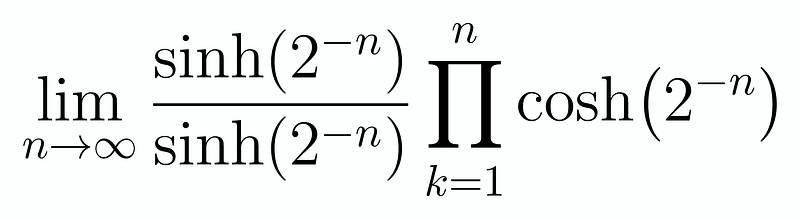
This leads us to:

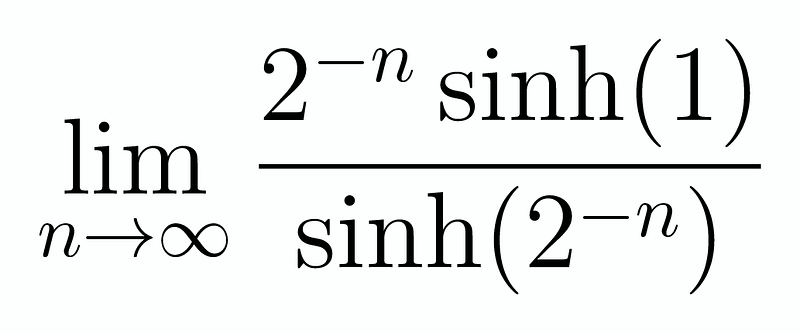
Next, we need to find a way to solve this limit. Here’s the clever technique. If we examine the series expansion for sinh(x), we have x + x³/3! + ... Given that 2^(-n) becomes very small as n approaches infinity, we can approximate sinh(2^(-n)) as 2^(-n). Therefore, this limit simplifies to:

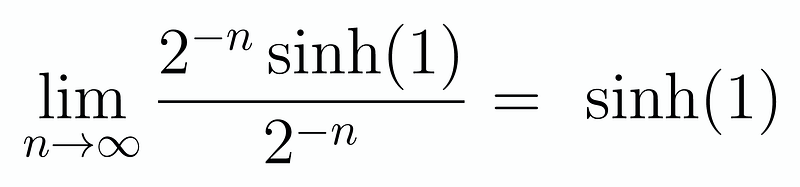
And that leads us directly to our solution! It's worth noting that we could replace our 1 with any x, and the outcome would still yield sinh(x)/x. A fascinating problem indeed! Thus, we arrive at:

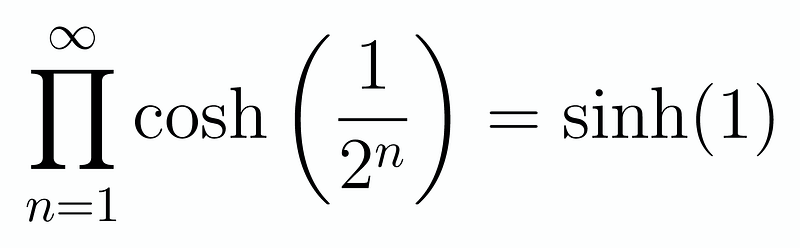
If you enjoyed this exploration, consider showing your support! It would mean a lot.