Engaging Calculus Challenge: Solve This Integral Puzzle!
Written on
Chapter 1: Introduction to the Puzzle
This intriguing challenge is suitable for anyone who has completed high school calculus!
If you recall fundamental integration techniques and basic algebra, you’re all set!
I suggest pausing here, grabbing some paper and a pen, and giving it a try. Once you're ready, continue reading for the solution!
Section 1.1: Understanding the Problem
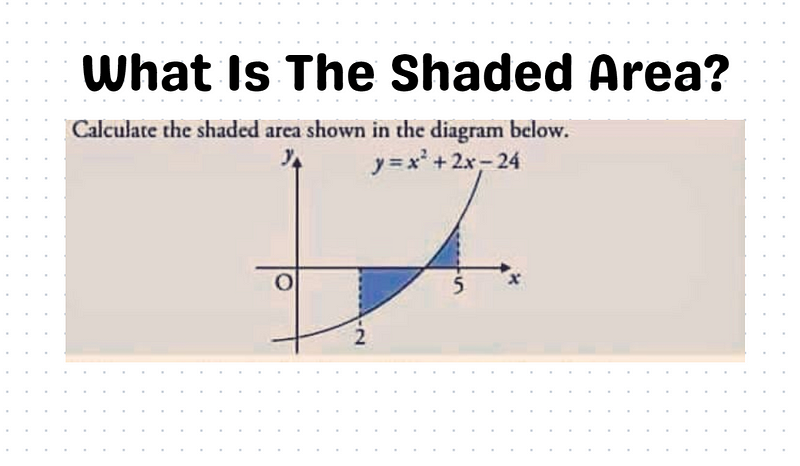
To tackle this problem, it's essential to determine where the curve intersects the x-axis. We achieve this by setting y to zero.
Upon performing factorization, we find:
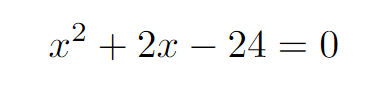
This calculation indicates that the curves meet the x-axis at -6 and 4.
Thus, we can conclude that the intersection depicted in the previous image is located at (4, 0).
With this information, we can compute the shaded area by evaluating the absolute value of the first section alongside the value of the second section.
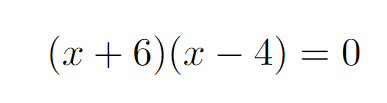
And there you have it—our final answer!

How fascinating is that?
What strategies did you use to solve it?
Please share your thoughts in the comments; I would love to hear from you!
The first video, "Let's Solve a Short Integral Puzzle," provides a detailed walkthrough of similar problems, making it accessible and engaging.
Section 1.2: Additional Resources
If you're interested in more challenges, consider checking out the best math puzzles featured on Medium, including topics like Algebra, Geometry, and more.
The second video, "Easy Calculus Problem - Anyone Can Understand!" is perfect for beginners and presents concepts in a straightforward manner.
Chapter 2: Conclusion
Thank you for engaging with this content!
Don't forget to show your appreciation if you found it insightful.
Your support means a lot to me as I continue to create valuable math resources.
Happy solving!

If you enjoyed this article, please consider buying me a coffee to support my writing efforts—it's greatly appreciated!