Understanding Classifiers

In the realm of classification, the target variable can assume distinct values known as “classes.” While regression focuses on predicting continuous values from a dataset, classification aims to predict these discrete outcomes.

We will explore three primary types of classifiers:

1. Generative classifiers: These models estimate the joint probability distribution of both input and target variables, denoted as Pr(x, t).
2. Discriminative classifiers: These focus on modeling the conditional probability of the target given an input variable, represented as Pr(t|x).
3. Distribution-free classifiers: These do not rely on a probability model but directly map inputs to target variables.

A brief note: terminology in this field can be perplexing, but we will clarify these concepts as we progress.

Generative vs. Discriminative Classifiers

The classifiers we will discuss include:

• Generative Classifiers: QDA, LDA, and Gaussian Naive Bayes—all specific cases of the same model.
• Discriminative Classifiers: Logistic regression.
• Distribution-Free Classifiers: The perceptron and support vector machines (SVM).

All these classifiers serve the same purpose (classification). However, determining the optimal model is not straightforward due to the “no free lunch” theorem, which suggests that no one model universally outperforms another across all datasets. Generally speaking, generative classifiers, like Naive Bayes, may excel with limited data, while logistic regression tends to perform better overall, particularly when data aligns with the assumptions of the generative model.

Most experts agree that discriminative models typically outperform generative ones. This is largely because generative models face a more complex task, as they attempt to model the entire joint distribution instead of merely the posterior. They often rely on assumptions that may not hold true for the data. Nevertheless, it’s crucial not to dismiss generative models entirely; for example, Generative Adversarial Networks (GANs) are generative models that have shown remarkable effectiveness in various applications.

Key Concepts in Classification

One foundational concept we will frequently reference is the multivariate Gaussian distribution, denoted as N(μ, Σ), where μ represents the mean vector and Σ the covariance matrix. The probability density function in D dimensions is defined as follows:

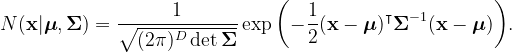
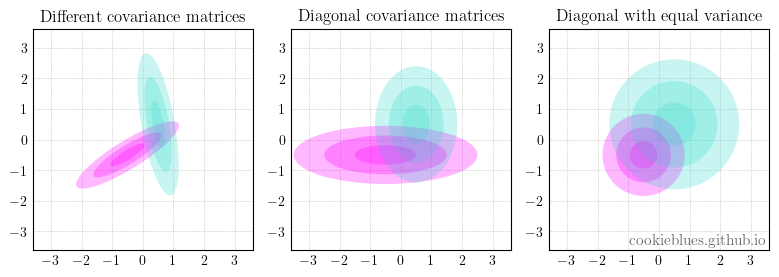
The covariance matrix is crucial as it defines the shape of the Gaussian distribution, which plays a significant role in the classifiers we will analyze. Below is an illustration of various covariance matrices.

Bayes' Theorem Explained

Another pivotal concept is Bayes' theorem. For those unfamiliar with frequentism versus Bayesianism, here’s a brief overview. Given two events A and B, we can express their joint probability using conditional probabilities:

Using the equation above, we can reformulate it to derive Bayes' theorem:

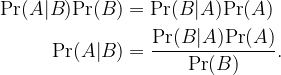
In the context of hypotheses and data, we often refer to the components of Bayes' theorem as posterior, likelihood, prior, and evidence.

This can be succinctly expressed as:

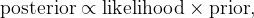
References

[1] Andrew Y. Ng and Michael I. Jordan, “On Discriminative vs. Generative classifiers: A comparison of logistic regression and naive Bayes,” 2001.

[2] Ilkay Ulusoy and Christopher Bishop, “Comparison of Generative and Discriminative Techniques for Object Detection and Classification,” 2006.